О понимании типов, абстракций данных и полиморфизма

От редакции

Как это ни удивительно, основные изыскания в компьютерной науке прошли в 60-70 годы прошлого столетия. Конечно, наука не стоит на месте, исследования ведутся и в наши дни, но они стали более специализированы, и оценить их значение может далеко не каждый. А вот то, что сейчас видно каждому, как раз и разрабатывалось в те годы. Одной из интересных областей исследования в компьютерной науке стали исследования в области систем типов и алгоритмов выведения типов. В этом номере мы публикуем посвященную этому вопросу статью, написанную в далеком 1985 году. Как ни странно, она до сих пор не потеряла актуальности.

Этот материал несколько выходит за рамки популярного изложения, но, по крайней мере, первая его часть будет наверняка полезна большинству читателей. Для тех, кто не знаком с математическими терминами, использованным в статье, или успел забыть их значение, приводятся краткие разъяснения во врезках.

1. От нетипизированной к типизированной вселенной

1.1.Организуя нетипизированную вселенную

Вместо вопроса «Что такое тип?», лучше зададимся вопросом, для чего вообще нужны типы в языках программирования. Чтобы ответить на этот вопрос, рассмотрим, откуда взялись типы в нескольких областях компьютерных наук и в математике. Путь от нетипизированного к типизированному проходили уже много раз в разных областях, и, в общем, по одинаковым причинам. Рассмотрим, например, следующие нетипизированные множества:

Битовые строки в памяти компьютера.

S-выражения (универсальные представления кода и данных – прим.ред.) в чистом Lisp.

λ-выражения в λ-исчислении.

Множества в теории множеств.

Самое конкретное – это битовые строки в памяти компьютера. ”Нетипизированное” реально значит, что есть только один тип. Здесь единственный тип – это слово в памяти, битовая строка фиксированного размера. Это нетипизированная вселенная, так как в ней абсолютно все должно быть представлено в виде битовой строки: символы, числа, указатели, структурированные данные, программы и т. д. При взгляде на часть памяти в общем невозможно сказать, что там находится. Смысл содержимого этого куска памяти определяется его внешней интерпретацией.

S-выражения в Lisp образуют другую нетипизированную вселенную, которая обычно строится поверх предыдущей – множества битовых строк. В ней не различаются программы и данные, и абсолютно все является теми или иными S-выражениями. У нас снова есть только один тип (S-выражение), хотя и более структурированный (можно различать атомы и cons-ячейки), и имеющий лучшие свойства, чем битовые строки.

В λ-исчислении все является (или должно представляться) функцией. Числа, структуры данных и даже битовые строки могут быть представлены как соответствующие функции. По-прежнему имеется только один тип: тип функции – из значений в значения, причем все значения сами являются функциями того же типа.

В теории множеств все является элементом или множеством элементов (или других множеств). Чтобы понять, насколько эта вселенная нетипиpована, нужно вспомнить, что почти вся математика, полная чрезвычайно богатых и сложных структур, представлена в теории множеств множествами, структурная сложность которых отражает сложность структур, представляемых с помощью этих множеств. Например, целые числа обычно представляются вложенными множествами с уровнем вложенности, представляющим кардинальность числа, функции представлены потенциально бесконечными множествами упорядоченных пар с уникальным первым значением.

Как только мы начинаем работать в нетипизированной вселенной, мы начинаем разными способами для разных целей организовывать ее. Поэтому в любой предметной области сами по себе, неформально, возникают типы – для классификации объектов по их поведению и использованию. Классификация объектов по целям их использования приводит к появлению более или менее хорошо определенной системы типов. Типы появляются естественно, даже в нетипизированных вселенных.

В памяти компьютера различают символы и операции, хотя и те, и другие представлены в виде битовых строк. В Lisp некоторые выражения называют списками, а другие образуют программы. В λ-исчислении некоторые функции должны представлять булевы значения, а другие – целые числа. В теории множеств некоторые множества служат для представления упорядоченных пар, а некоторые множества упорядоченных пар называют функциями.

λ-исчисление

В λ-исчислении каждое выражение означает функцию с одним аргументом, аргумент функции, в свою очередь, тоже функция с одним аргументом, а значение функции – еще одна функция с одним аргументом. λ-выражение фактически определяет анонимную функцию, выражая действие функции над ее аргументом. Например, функция f, «плюс два», f(x) = x + 2, в λ-исчислении может быть выражена как λ x. x + 2 (или, что то же самое, λ y. y + 2, так как имена формальных аргументов не имеют значения), а вызов функции, например, f(3), будет выглядеть как (λ x. x + 2) 3. Применение функции левоассоциативно: f x y = (f x) y. Рассмотрим функцию, принимающую функцию как аргумент и применяющую ее к числу три: λ f. f 3. Последнюю функцию модно применить к упоминавшейся функции «плюс два»: (λ f. f 3) (λ x. x+2). Следующие три выражения эквивалентны:

(λ f. f 3) (λ x. x + 2)

(λ x. x + 2) 3

3 + 2

То, что λ-выражение не может иметь более одного аргумента, компенсируется тем, что оно может ссылаться на аргументы λ-выражения, в которое оно вложено. Например, функцию f(x, y) = x – y можно выразить как λ x. λ y. x - y. Таким образом, λ- выражение поддерживает замыкание на внешний лексический контекст.

В данной статье автор использует нотацию fun (список параметров) для описания λ-выражений. При этом его система записи позволяет создавать λ-выражения с более, чем одним аргументом.

Нетипизированная вселенная объектов вычислений естественным образом распадается на подмножества объектов с одинаковым поведением. Множества объектов с одинаковым поведением можно назвать и рассматривать как типы. Например, постоянство поведения целых чисел состоит в том, что к ним можно применить одно и тоже множество операций. Для функций постоянное поведение состоит в том, что они могут применяться к объектам данного типа и возвращать значения данного типа. Подробнее см. http://en.wikipedia.org/wiki/Lambda_calculus

Приложив героические организационные усилия, мы можем начать думать о нетипизированных вселенных как о типизированных. Но это только иллюзия, поскольку только что созданную структуру типов очень легко разрушить. Что в Lisp будет результатом обращения к произвольному S-выражению как к программе? Каков в λ-исчислении будет эффект применения условного выражения к не булевому значению? Какое объединение множеств будет в теории множеств являться функцией получения последующего элемента, а какое – функцией получения предыдущего элемента.

Такие вопросы – следствие неудачной попытки организовать нетипизированную вселенную, не проходя всего пути к типизированным системам; поэтому есть смысл обратиться к более высокоуровневым концепциям и их взаимодействию.

1.2 Статическая и строгая типизация

Основная цель системы типов – обойти вопрос о представлениях и исключить ситуации, когда такие вопросы могут возникнуть. В математике, как и в программировании, типы накладывают ограничения, помогающие соблюсти корректность. Некоторые нетипизированные вселенные, такие, как наивная теория множеств, оказываются логически противоречивыми. Типизированные версии этой теории позволяют устранить противоречия. Типизированные версии теории множеств, так же, как и типизированные языки программирования, накладывают ограничения на взаимодействия между объектами, предотвращая противоречия при взаимодействии объектов (в данном случае множеств) с другими объектами.

Типы могут рассматриваться как набор одежды (или защиты), которая защищает нижележащую нетипизированную систему от произвольного или незапланированного использования. Эта “одежда” образует защитный слой, скрывающий нижележащее представление, и ограничивает способы взаимодействия объектов. В нетипизированной системе нетипизированные объекты обнажены, то есть нижележащее представление системы открыто всем. Нарушение системы типов означает удаление защитного слоя и действия непосредственно над беззащитным представлением.

Объекты некоторого типа имеют представление, отражающее ожидаемые свойства типа данных. Представление должно облегчать выполнение ожидаемые операции над объектами данных. Например, позиционная нотация удобна для чисел, так как позволяет просто определить арифметические операции. Однако при выборе представления данных существует много возможных вариантов. Нарушение системы типов позволяет манипулировать представлениями данных произвольными способами, с потенциально разрушительным результатом. Например, использование целого числа в качестве указателя может стать причиной случайных изменений в программах или данных.

Чтобы предотвратить нарушение типов, мы, как правило, навязываем программам статическую структуру типов. Типы ассоциируются с константами, операторами, переменными и функциями. Если недостаточно или отсутствует явная информация о типах, для вывода типов выражений может быть использована система вывода типов (type inference). В таких языках, как Паскаль и Ада, типы переменных и функциональных символов определены избыточными декларациями, и компилятор может проверить последовательность определения и использования. В таких языках, как ML, явные объявления исключены, где это только возможно, и система может вывести тип выражения по локальному контексту, одновременно поддерживая непротиворечивость использования.

Языки программирования, в которых тип любого выражения может быть определен с помощью статического анализа программы, называются статически типизированными. Статическая типизация – это полезное свойство, но требование привязки всех переменных и выражений к типом во время компиляции иногда накладывает чрезмерные ограничения. Его можно заменить более мягким требованием, чтобы все выражения гарантировано имели тип, хотя сам тип может быть статически неизвестен; этого в общем случае можно добиться, добавив некоторые проверки во время исполнения. Языки, в которых все выражения имеют совместимые типы, называются строго типизированными языками. Если язык строго типизирован, его компилятор может гарантировать, что принимаемая им программа будет выполняться без ошибок, связанных с типами. В общем случае стоит бороться за строгую типизацию, и использовать статическую типизацию везде, где это возможно. Заметьте, что каждый статически типизированный язык является строго типизированным, но обратное необязательно верно.

Статическая типизация позволяет выявить несовместимость типов при компиляции и гарантирует, что исполняемая программа не содержит несовместимости типов. Это помогает как можно раньше находить ошибки типов и повышает эффективность работы программы. Это дисциплинирует программиста, результатом чего являются более структурированные и удобочитаемые программы. Но статическая типизация может также привести к потере гибкости и выразительности из-за преждевременного ограничения поведения объектов до поведения, ассоциированного с конкретным типом. Традиционные статически типизированные системы исключали использование приемов программирования, которые, при всей их безупречности, противоречат раннему связыванию объектов программы с определенным типом. Например, они исключают использование обобщенных функций, например, сортировки, в которых структура алгоритма одинаково применима к разным типам.

1.3 Виды полиморфизма

Традиционные типизированные языки, например Паскаль, основаны на идее, что функции и процедуры, и, следовательно, их операнды имеют уникальный тип. Такие языки называются мономорфными (monomorphic), в том смысле, что каждая значение и переменная могут интерпретироваться как один и только один тип. Мономорфные языки программирования могут быть противопоставлены полиморфным (polymorphic) языкам, в которых некоторые значения и переменные могут иметь более одного типа. Полиморфные функции – это функции, чьи операнды (фактические параметры) могут иметь более одного типа. Полиморфные типы – это типы, операции над которыми применимы к значениям более чем одного типа.

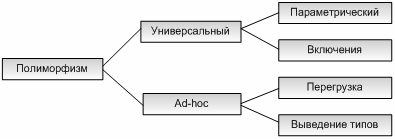
Рисунок 1. Варианты полиморфизма.

Straychey [67] неформально определил два главных типа полиморфизма.

В случае параметрического полиморфизма функция одинаково работает с некоторым диапазоном типов: эти типы, как правило, имеют сходную структуру. Перегрузка (ad-hoc polymorphism) проявляется, если функция работает (или выглядит работающей) с несколькими разными типами (которые могут и не иметь общей структуры) и может вести себя различным образом в разных случаях.

Наша классификация полиморфизма (рисунок 1) развивает классификацию Strachey, вводя новую форму полиморфизма, полиморфизм включения (inclusion polymorphism), для моделирования подтипов и наследования. Параметрический полиморфизм и полиморфизм включения классифицированы как две главных подкатегории универсального полиморфизма, который противопоставлен не универсальному полиморфизму (перегрузке). Таким образом, рисунок 1, отражая точку зрения Strachey на полиморфизм, добавляет полиморфизм включения для моделирования объектно-ориентированного программирования.

Параметрический полиморфизм называется так потому, что единообразие структур типов обычно достигается с помощью параметров типов, но единообразия можно добиться разными способами, и эта более общая концепция называется универсальным полиморфизмом. Универсально полиморфные функции будут нормально работать с бесконечным количеством типов (имеющих некоторую общую структуру), а перегруженные функции будут работать только с конечным множеством разных и потенциально несвязанных типов. В случае универсального полиморфизма можно с уверенностью заявить, что некоторые значения имеют много типов, что трудно поддерживать в случае перегруженных функций, и, с некоторой точки зрения, функции перегрузки – это небольшое множество мономорфных функций. В смысле реализации универсальные полиморфные функции будут выполнять один и тот же код для аргументов всех допустимых типов, тогда как перегруженные функции могут исполнять разный код для каждого типа аргументов.

Существует два основных типа универсального полиморфизма, то есть два пути, при которых значение может иметь много типов. При параметрическом полиморфизме полиморфная функция имеет явный или неявный параметр типа, определяющий тип аргумента при каждом применении этой функции. При полиморфизме включения объект можно рассматривать как принадлежащий многим различным классам, не обязанным быть непересекающимися, то есть может иметь место вложение классов. Эти два представления универсального полиморфизма взаимосвязаны, но достаточно существенно отличаются практически и теоретически, чтобы заслужить различные названия.

Функции, обладающие параметрическим полиморфизмом, также называются обобщенными, или generic-функциями. Например, функция длины (length), принимающая значения из списка произвольных типов и возвращающая целые числа, называется обобщенной функцией длины. Обобщенная функция – это такая функция, которая может работать с аргументами различных типов, в общем случае выполняя одну и ту же работу независимо от типа аргумента. Если рассматривать обобщенную функцию как одно значение, она будет иметь много функциональных типов, и, таким образом, будет полиморфной. Обобщенные функции Ada – особый случай этой концепции.

Есть также два основных типа перегрузок. При перегрузке одно и то же имя используется для разных функций, и то, какая функция соответствует конкретному имени, определяется по контексту. Можно предполагать, что при предварительной обработке программы перегрузка будет удалена, и различным функциям будут присвоены различные имена. В этом смысле перегрузка – это просто удобное синтаксическое сокращение. Приведение типов (coercion) – это, наоборот, семантическая операция, необходимая для того, чтобы преобразовать аргумент в тип, которого ожидает функция, в ситуации, которая иначе привела бы к ошибке. Приведения типов могут быть реализованы статически, путем их автоматической вставки в код во время компиляции, или динамически, при проверках типов аргументов во время исполнения.

Различие между перегрузкой и приведением в некоторых ситуациях размыто. Это в частности верно, когда мы рассматриваем нетипизированный или интерпретируемый язык. Но даже в статически типизированных, компилируемых языках может возникнуть путаница между двумя формами перегрузочного полиморфизма, как показывает следующий пример:

3 + 4

3.0 + 4

3 + 4.0

3.0 + 4.0

Здесь перегрузочный полиморфизм оператора + можно объяснить одним из следующих способов:

§         Оператор + имеет 4 перегруженных варианта, по одному для каждой из четырех комбинаций типов аргументов.

§         Оператор + имеет 2 перегруженных варианта, соответствующих сложению целых и действительных чисел. Если один из аргументов – типа «целое число», а другой – типа «действительное», аргумент типа «целое» приводится к типу «действительное».

§         Оператор + определен только для сложения действительных чисел, и целые аргументы всегда будут приводиться к соответствующим значениям действительных чисел. В этом примере одно и то же выражение можно рассматривать как представляющее и перегрузку, и приведение типов, и как оба сразу, в зависимости от реализации.

Наше определение полиморфизма применимо только к языкам с очень четкими понятиями типа и значения. В частности, нужно различать присущий объекту тип и видимый тип его синтаксического представления в языках, разрешающих перегрузку и приведение типов. Эти вопросы подробнее разбираются ниже.

Если рассматривать тип как частично определяющий поведение или предполагаемое использование ассоциированных с типом значений, то мономорфная система типов ограничивает объект единственным поведением, а полиморфная система типов позволяет ассоциировать значения с более чем одним поведением. Выразительность строго мономорфных языков очень ограничена, так как они не позволяют значениям или даже синтаксическим символам, определяющим значения, иметь различное поведение в различном контексте использования. Такие языки, как Паскаль и Ада, имеют способы ослабления строгого мономорфизма, но полиморфизм в них – скорее исключение, нежели правило, и можно назвать их почти мономорфными. Реальные и мнимые исключения из мономорфной типизации в обычных языках включают в себя:

Перегрузка: целочисленные константы могут иметь как тип integer, так и тип real. Такие операторы, как +, применимы к аргументам как типа Integer, так и типа real.

Приведение типов: значения типа integer могут использоваться там, где ожидается значение типа real, и наоборот.

Выделение подтипов: элементы, принадлежащие к поддиапазону типов, принадлежат также к диапазону типов, содержащий этот поддиапазон.

Совместное использование значений: nil в Паскаль – это константа, которая совместно используется всеми типами указателей.

Эти четыре примера, которые могут сосуществовать в одном и том же языке, являются примерами четырех совершенно разных способов расширения мономорфной системы типов. Давайте посмотрим, как они укладываются в приведенные выше определения различных типов полиморфизма.

Перегрузка – это чисто синтаксический способ использования одного и того же имени для различных семантических объектов; компилятор может разрешить неоднозначность во время компиляции.

Приведение типов позволяет пользователю опускать семантически необходимые преобразования типов. Необходимые преобразования типов должны определяться системой, быть встроенными в программу и использоваться компилятором для генерации кода необходимых преобразований типов. Приведение типов – это, в сущности, сокращение размера кода, которое может уменьшить размер и улучшить читаемость программы, но оно может также порождать незаметные и порой опасные ошибки в системе. Необходимость приведения типов времени исполнения обычно определяется во время компиляции, но в таких языках, как (не чистый) Lisp, встречается множество приведений, распознаваемых и обрабатываемых только во время исполнения.

Выделение подтипов – это случай полиморфизма включения. Идея о том, что типы могут быть подтипами других типов, причем не только в случае поддиапазонов упорядоченных типов, таких, как integer, но и в случае более сложных структур. Например, тип Тойота может являться подтипом типа Транспортное средство. Каждый объект подтипа может быть использован в контексте супертипа в том смысле, что каждая Тойота – это транспортное средство, и к ней применимы любые операции, применимые к транспортным средствам.

Совместное использование значений – это частный случай параметрического полиморфизма. Можно подумать, что символ nil имеет большое количство перегрузок, но это было бы странной неокончательной перегрузкой, так как nil – это элемент бесконечного множества типов, в том числе и еще не объявленных. Более того, любое использование элемента nil означает одно и то же значение, что нетипично для перегрузки. Можно также подумать, что для каждого типа есть свой nil, но все эти nil имеют одинаковое представление и могут быть идентифицированы. Тот факт, что объект, имеющий много типов, одинаково представляется для всех типов – это характеристика параметрического полиморфизма.

Какое отношение к полиморфизму имеют эти ослабленные формы типизации? Как неявно предполагается из названия, универсальный полиморфизм считается истинным полиморфизмом, тогда как перегрузочный полиморфизм – это некоторый вид кажущегося полиморфизма, чья полиморфная натура при ближайшем рассмотрении исчезает. Перегрузка не является истинным полиморфизмом: вместо значения, имеющего много типов, мы позволяем символу иметь много типов, но значения, определяемые этими символами, имеют различные и возможно несовместимые типы. Приведение типов также не является истинным полиморфизмом: оператор может выглядеть, как принимающий значения многих типов, но значения должны быть приведены к некоторому представлению, прежде чем оператор сможет использовать их; таким образом, оператор работает только с одним типом. Более того, выдаваемый тип больше не зависит от исходного типа, как в случае параметрического полиморфизма.

В противоположность перегрузке и приведению типов, выделение подтипов – это пример истинного полиморфизма: объектами подтипа можно единообразно манипулировать так, как если бы они принадлежали к супертипам. В реализации представление выбирается очень тщательно, поэтому никаких приведений типов при использовании объекта подтипа вместо объекта супертипа не требуется. В этом смысле один объект может иметь много типов (например, в Simula член подкласса может иметь больший сегмент памяти, нежели член его суперкласса, а его начальный сегмент имеет ту же структуру, что и у члена суперкласса). Сходным образом, операции должны единообразно интерпретировать представления, чтобы одинаково работать с элементами подтипов и супертипов.

Параметрический полиморфизм – это самая чистая форма полиморфизма; один и тот же объект или функция может единообразно использоваться в различных контекстах типов без изменений, приведений, каких-либо проверок времени выполнения или перекодировки представления. Однако следует заметить, что такая единообразность поведения требует, чтобы все данные были представлены, или каким-то образом рассматривались, единообразно (например, по указателю).

Четыре рассмотренных к этому моменту способа ослабления мономорфной типизации становятся мощнее и интереснее, если рассматривать их в связке с операторами, функциями и процедурами. Рассмотрим некоторые примеры. Символ + может быть перегружен для использования в одно и то же время при сложении типов integer и real, и при конкатенации строк. Использование одного и того же символа для всех трех операций отражает примерное сходство алгебраической структуры, но нарушает требования мономорфности. Неоднозначность можно разрешить по типам операндов перегруженного оператора, но этого может оказаться недостаточно. Например, если 2 перегружено для определения целого 2 и действительного 2.0, то 2+2 останется неопределенным, и разрешается это только в более широком контексте, таком, как присваивание типизированной переменной. Набор возможностей может взрывоподобно увеличиться, если разрешить пользовательскую перегрузку операторов.

Алгол 68 хорошо известен своей причудливой формой приведения типов. Решаемые в нем проблемы очень схожи с перегрузкой, но вдобавок, приведения типов вызывают последствия во время исполнения. Двумерный массив с единственной строкой может быть приведен к вектору, а вектор с единственным элементом может быть приведен к скаляру. Условия выполнения приведения типов могут быть выявлены во время выполнения, причем могут быть не запланированными, а появившимися из-за ошибок программирования. Пример Алгола 68 показал, что приведение типов в общем должно быть явным, и этот взгляд восторжествовал в дизайне многих более поздних языков.

Полиморфизм включения можно найти во многих языках, самым ранним примером может служить Simula 67. Классы Simula – это определенные пользователем типы, организованные в простую иерархию наследования, где каждому классу соответствует единственный непосредственный суперкласс. Объекты и процедуры Simula полиморфны, так как объекты подкласса могут использоваться там, где требуется объект одного из его суперклассов. Smalltalk [Goldberg 83] – это не типизированный язык, но он внес свой вклад в популяризацию такого взгляда на полиморфизм. Недавно Lisp Flavors [Weinreb 81] (нетипизированный) расширил этот стиль полиморфизма до множественных непосредственных суперклассов, а Amber (типизированный) [Cardelli 85] еще более расширил – до функций высшего порядка.

Полнее всего парадигма параметрического полиморфизма представлена в языке ML [Milner 84], который изначально был построен вокруг этого стиля типизации. В ML можно написать полиморфную функцию identity, работающую с любыми типами аргументов, а также функцию length, которая отображает список с элементами произвольного типа на целое число. Можно также создать обобщенную функцию сортировки, работающую с любыми типами. Другие языки, использовавшие эти идеи или способствовавшие их развитию – это CLU [Liskov 81], Russell [Demers 79, Hook 84], Hope [Burstall 80], Ponder [Fairbairn 82] and Poly [Matthews 85].

Наконец, нельзя не упомянуть обобщенные процедуры, подобные имеющимся в Ada. Это параметризированные шаблоны, которым должны быть назначены значения параметров перед использованием. Полиморфизм обобщенных процедур Ada похож на параметрический полиморфизм таких языков как ML, но ограничен до конкретных видов параметров. Эти параметры могут быть типами, процедурами или просто значениями. Обобщенные процедуры с параметрами типов полиморфны в том смысле, что формальные параметры типов могут принимать значения различных типов в различных реализациях. Однако полиморфизм обобщенных типов в Ada – синтаксический, так как обобщенная реализация выполняется во время компиляции с конкретными значениями типов, которые должны быть определимы (через манифест) во время компиляции. Семантика обобщенных процедур – это макрорасширение, управляемое типами аргументов. Поэтому обобщенные процедуры можно рассматривать как аббревиатуры для наборов мономорфных процедур. В отношении же полиморфизма, достоинство обобщенных процедур состоит в том, что для разных форм исходных данных может быть сгенерирован оптимальный специализированный код. С другой стороны, в истинно полиморфных системах для каждой обобщенной процедуры код генерируется только один раз.

1.3 Эволюция типов в языках программирования

В ранних языках программирования вычисления ассоциировались с числовыми вычислениями, а значения имели единственный арифметический тип. Однако еще в 1954 в Фортране сочли удобным различать типы integer и float, отчасти потому, что различия в аппаратном представлении делали работу с целыми числами более экономичной, а отчасти из-за того, что использование integer для итераций и вычислений с массивами логически отличалось от использования в расчетах чисел с плавающей запятой.

В Фортране целочисленные переменные и переменные с плавающей запятой различались по первой букве имени. Алгол 60 сделал это различие явным, введя объявление дополнительных идентификаторов для переменных с типами Integer, real и Boolean. Алгол 60 был первым из заслуживающих внимания языков, имевших явное определение типа и соответствующие требования для проверки типов при компиляции. Его требования к структуре блоков позволяли при компиляции проверять не только типы, но и область видимости переменной.

Понятие типа в Алгол 60 в шестидесятых было расширено до более богатых классов значений. Из многочисленных типизированных языков, разработанных в те времена, за вклад в эволюцию языков программирования заслуживают внимания PL/I, Паскаль, Алгол 68 и Simula.

PL/I пытался объединить возможности Фортрана, Алгола, Кобола и Лиспа. В него включены такие типы, как типизированные массивы, записи и указатели. Но типизация в нем была довольно дырявой: например, не требовалось определять тип значений, на который указывает указатель, что ослабляло эффективность проверки типов при компиляции.

В Паскаль система типов расширена до массивов, записей, указателей и типов, определенных пользователем. Однако Паскаль не определяет эквивалентность типов, поэтому ответ на вопрос, когда два выражения определяют один и тот же тип, зависит от реализации. Есть проблемы и с гранулярностью типов. Например, определение типа массив в Паскале, которое включает границы массива как часть типа, не позволяет создавать процедуры, одинаково оперирующие с массивами разной размерности. Паскаль оставляет лазейки в строгих определениях типов, не требуя указывать полный тип процедур, передаваемых в качестве параметров, и позволяя независимо манипулировать полями признаков вариантной записи. Эти неоднозначности и в системе типов Паскаля обсуждаются в [Welsh 77].

Определения типов в Алгол 68 строже, чем в Паскале, причем хорошо определено понятие эквивалентности типов (структурной эквивалентности). Понятие типа (имеет название mode в Алгол 68) расширено за счет включения процедур как значений первого класса. Простейшие типы включают Int, real, char, bool, string, bits, bytes, format, file, а конструкторы типов включают array, struct, proc, union и ref соответственно для конструирования таких типов, как массив, запись, процедура и указатель. В Алгол 68 подробно определены правила преобразования типов, использования разыменований, распроцедурирования, расширения, укрупнения, объединения и низведения для преобразования значений к типам, нужным для дальнейших вычислений. Проверка типов в Алголе 68 разрешима, но алгоритм проверки типов настолько сложен, что пользователь не всегда может справиться с вопросами эквивалентности и преобразования типов. Эту сложность некоторые сочли недостатком, что привело к протестам против сложных систем типов. Поэтому в более поздних языках, например, в Ada, использовалось более простое определение эквивалентности типов с существенно ограниченным преобразованием типов.

Симула – это первый объектно-ориентированный язык. Понятие типа в нем включает классы, чьи экземпляры можно присвоить классовым переменным, и которые могут сохраняться между исполнением содержащихся в них процедур. Определения процедур и данных класса составляют его интерфейс и доступны пользователю. Подклассы наследуют сущности, объявленные в интерфейсе суперкласса, и могут определять дополнительные операции и данные, конкретизирующие поведение подкласса. Экземпляры класса напоминают абстракции данных - у них есть интерфейс и состояние, сохраняемое между вызовами операций, но отсутствует механизм сокрытия информации, имеющийся у абстракций данных. Такие появившиеся позже объектно-ориентированные языки, как Smalltalk и Loops, объединили унаследованную от Симулы концепцию классов со строгим определением сокрытия информации.

Модула-2 стал первым широко распространенным язык, использовавшим модульную компоновку как основной принцип структурирования. Типизированные интерфейсы определяют типы и операции, доступные в модуле; типы в интерфейсе могут быть непрозрачными (opaque) для реализации абстракций данных. Интерфейс может быть определен отдельно от реализации, тем самым разделяя задачи спецификации и реализации. Используемые в блоках области видимости, поддерживаемые на уровне модулей, на более высоком уровне заменяются гибкими межмодульными правилами видимости, реализуемыми с помощью списков импорта и экспорта. Интерфейсы модулей похожи на объявления классов (за исключением упомянутых правил области видимости), но, в отличие от экземпляров классов, экземпляры модулей не являются значениями первого класса. Фаза линковки необходима, чтобы связать экземпляры модулей для исполнения; эта фаза определяется модульными интерфейсами, но является внешней по отношению к языку.

ML внес в языки понятие параметрического полиморфизма. Типы ML могут содержать переменные типов, которым в разных контекстах могут быть приписаны разные типы. Следовательно, можно указывать информацию о типах частично, и писать программы, основанные на частично определенных типах, и применимые к любым экземплярам этих типов. Частичное определение типов нужно для того, чтобы опустить объявление типов: наиболее общие типы, удовлетворяющие данной ситуации, выводятся автоматически.

Приведенный выше исторический экскурс дает основу для дальнейшего обсуждения отношений между типами, абстракциями данных и полиморфизмом в реальных языках программирования. Мы рассмотрим нетипизированные абстракции данных (пакеты) в Ада, укажем влияние на методологию требований наличия у абстракций данных типа и наследования, обсудим интерпретацию наследования как полиморфизма выделения подтипов, а также связь между полиморфизмом подтипов в Smalltalk и параметрическим полиморфизмом в ML.

Ада содержит разнообразнейшие модули, включая подпрограммы для поддержки процедурно-ориентированного программирования, пакеты для поддержки абстракций данных и задачи для поддержки параллельного программирования. Но у нее относительно слабое определение типа, исключающее из множества типизированных объектов процедуры и пакеты, и относительно поздно включающее типы задач в процесс дизайна. Выбор в качестве эквивалентности типов эквивалентности имен слабее, чем идея структурной эквивалентности, использовавшаяся в Алгол 68. Строгий запрет неявного приведения типов ослабляет возможность предоставления полиморфных операций применимых к операндам многих типов.

Пакеты в Ада содержат интерфейсное определение именованных членов, которые могут быть простыми переменными, процедурами, исключениями и даже типами. Они могут прятать своё локальное состояние, либо с помощью скрытого типа данных, либо в теле пакета. Пакеты похожи на экземпляры записей в том, что имеют интерфейс именованных членов. Пакеты Ада отличаются от записей тем, что члены записей должны быть типизированными значениями, а члены пакетов могут быть процедурами, исключениями, типами или другими именованными сущностями. Поскольку пакеты – это не типы, они не могут быть параметрами, членами структур или значениями указателей [Wegner 83]. Пакеты в Ада – это второстепенные сущности, тогда как экземпляры классов в Simula или объекты в объектно-ориентированных языках – это первоклассные сущности.

Различия поведения пакетов и записей в Ада устраняются в объектно-ориентированных языках расширением понятия типа на процедуры и абстракции данных. В контексте этого обсуждения полезно определить объктно-ориентированные языки как расширение процедурных языков, поддерживающее типизированные абстракции данных с наследованием. Итак, можно сказать, что язык объектно-ориентированный, если он удовлетворяет следующим требованиям:

§         Он поддерживает объекты, являющиеся абстракциями данных с интерфейсом именованных операций и сокрытием локального состояния.

§         Объекты имеют соответствующий объектный тип.

§         Типы могут наследовать атрибуты супертипов.

Эти требования можно суммировать следующим образом:

Объектно-ориентированность = абстракции данных + объектные типы + наследование типов.

Полезность этого определения можно проиллюстрировать, рассмотрев влияние каждого из этих требований на методологию. Абстракции данных сами по себе предоставляют способ организации данных с соответствующими операциями, что сильно отличается от традиционной методологии процедурных языков. Реализация методологии абстракций данных была одной из главных целей Ада, и эта методология описывается в литературе по Ада [Booch, 83]. Однако Ада удовлетворяет только первому из трех требований объектно-ориентированного программирования, и интересно было бы рассмотреть влияние объектных типов и наследования на методологию абстракций данных [Hendler 86].

Требование типизации всех объектов позволяет объектам быть первостепенными значениями, поэтому язык позволяет управлять ими как структурами данных, а также использовать в вычислениях. Требование наследования типов разрешает определять отношения между типами. Наследование можно рассматривать как механизм формирования типов, позволяющий использовать свойства одного или более типов в определениях другого типа. Определение «B наследует A» можно рассматривать как механизм упрощения, исключающий переопределение атрибутов типа А в определении B. Однако наследование – это больше, чем сокращение, так как оно создает из коллекции связанных типов структуру, которая может значительно снизить концептуальную сложность спецификации системы. В [Goldberg 83] это показано на примере объектной иерархии Smalltalk.

Иерархия объектов в Smalltalk – это описание среды программирования Smalltalk. Концептуально это похоже на функцию apply в Lisp, описывающую интерпретатор языка Lisp на Lisp же, но гораздо сложнее. Она описывает иерархию наследования в коллекции более 75 связанных системных объектов. Объектные типы включают числовые объекты, структурированные объекты, объекты ввода-вывода, параллельные и т.д. Объектная иерархия выносит свойства общие для всех числовых объектов в супертип Number. Свойства, общие для разных видов списков, выносятся в супертип Collection. Далее общие свойства чисел, структур и других видов объектов выносятся в супертип Object. Таким образом, коллекция более 75 объектных типов, составляющих среду Smalltalk, описывается как относительно простая структурированная иерархия объектных типов. Упрощение, предоставляемое иерархией объектов при повторном использовании суперклассов, чьи атрибуты совместно используются подклассами, неожиданно дает серьезную экономию.

Объектная иерархия Smalltalk также имеет значение в качестве иллюстрации возможностей полиморфизма. Мы можем описать полиморфную функцию как функцию, применимую к значениям более, чем одного типа, а полиморфизм включения (inclusion polymorphism) – как отношение между типами, которое разрешает применение операций к объектам разных типов, связанных включением. Объекты рассматриваются как коллекции таких полиморфных операций (аттрибутов). Такой подход подчеркивает, что совместное использование операций операндами разных типов – главная черта полиморфизма.

Иерархия объектов Smalltalk реализует описанную выше разновидность полиморфизма, вынося все общие для набора подтипов атрибуты в некоторый супертип. Атрибуты, общие для числовых типов, вынесены в супертип Number. Общие атрибуты коллекций вынесены в супертип Collection. Общие для всех типов атрибуты вынесены в супертип Object. Таким образом, полиморфизм тесно связан с понятием наследования, и можно сказать, что выразительность системы типов в значительной степени обусловлена используемым ей полиморфизмом.

Чтобы закончить обсуждение эволюции типов в языках программирования, рассмотрим механизм типов в ML [Milner 84]. ML – это интерактивный функциональный язык программирования, в котором пропущенные пользователем спецификации типов могут быть выведены. Если пользователь вводит “3+4”, система отвечает “7:int”, вычисляя значение выражения, и выводит, что операнды и выражение в целом имеют тип int. Если пользователь вводит объявление функции “fun f x = x + 1”, то система отвечает “f:Int → int”, определяя значение функции f, и выводит её тип “int → int”. ML поддерживает выведение типов не только для традиционных типов, но также для параметрических (полиморфных) типов, например таких, как функция длины списков. Если ввести “fun rec length x = if x = nil then 0 else 1 + length(tail(x));”, то ML выведет, что length – это функция списка элементов произвольного типа, возвращающая integer (length:’a list → int). Если пользователь затем вводит “length[1;2;3]”, применяя length к списку целых чисел, то система выводит, что length имеет конкретный тип “int list → int” и потом применяет конкретную функцию к списку целых.

Говоря, что параметрическая функция применима к спискам произвольного типа, мы на самом деле имеем в виду, что этот тип может быть специализирован некоторым (явно или неявно) предоставленным параметром T, и что специализированная функция может быть применена к конкретным операндам. Между параметрической функцией length для списков произвольного типа и специальной функцией для списков типа Int есть важное различие. Такие функции, как length, применимы к спискам произвольных типов, поскольку эти типы имеют одинаковое представление параметров, что позволяет специализировать их, указав параметр типа. Это различие между параметрическими функциями и их конкретными версиями в таких языках, как ML, размыто, так как параметры типов, пропущенные пользователем, автоматически выводятся механизмом выведения типов.

Супертипы в объектно-ориентированных языках можно рассматривать как параметрические типы, чьи параметры не указаны пользователем. Чтобы понять сходство супертипов и параметрических типов, полезно ввести нотацию, где параметры супертипов должны быть явно указаны при конкретизации супертипа для получения подтипа. Ниже будет показано, что у Fun есть явные параметры типов как для параметрических типов, так и для супертипов, для предоставления единой модели как параметрического полиморфизма, так и полиморфизма выделения подтипов. Это приводит к одинаковой трактовка выведения типов при недостаче параметров как для параметрических типов, так и для супертипов.

1.5. Подъязыки для выражения типов

По мере того, как множество типов языка программирования становится богаче, а набор определяемых типов становится бесконечным, становится полезным определять множество типов при помощи подъязыка выражения типов. Множество выражений типов современного строго типизированного языка программирования, в общем, представляет собой простое, однако не очень тривиальное подмножество этого языка. Подъязыки для выражения типов в общем случае включают такие базовые типы, как integer и Boolean, и такие составные типы, как массивы, записи и процедуры, составленные из базовых типов.

Type ::= BasicType | ConstructedType

BasicType ::= Int | Bool | ...

ConstructedType ::= Array(Type) | Type → Type | ...

Подъязык для определения типов должен быть достаточно богатым, чтобы поддерживать типы всех обрабатываемых значений, и достаточно гибким, чтобы обеспечить эффективную проверку типов. Одна из целей этой статьи – поиск компромисса между богатством и гибкостью подъязыка выражения типов в строго типизированных языках.

В целом подъязык для выражения типов может быть определен с помощью контекстно-независимой грамматики. Однако нас интересует не только синтаксис подъязыка, но и его семантика. Поэтому нас интересует и то, какие типы определять, и отношения между выражениями типов. Самое основное отношение между выражениями типов – это эквивалентность типов. Однако нас интересуют также и отношения подобия типов, которые слабее, чем отношения эквивалентности, например, включение, которое связано с выделением подтипов. Отношения подобия между выражениями типов, позволяющие выражениям типов определять более одного типа, или быть совместимыми со многими типами, относится к полиморфизму.

Полезность системы типов не только в представляемом с ее помощью наборе типов, но и в возможностях выражения различных видов отношений между типами. Возможность выражать отношения между типами включает возможность выполнять вычисления с типами, чтобы определить, удовлетворяют ли они предъявленным требованием. Такие вычисления могут в принципе быть не менее мощными, чем вычисления, выполняемые со значениями. Однако нас волнуют только простые, легко рассчитываемые отношения, выражающие единообразное поведение коллекции типов.

Читатель, интересующийся обсуждением создания языка выражения типов и алгоритмов для проверки типов в таких языках, как Паскаль и С, могут прочитать главу 6 в [Aho 85], где рассматриваются проверки типов при перегрузках, приведении типов и параметрическом полиморфизме. Fun добавляет к набору базовых типов абстрактные типы данных, и добавляет подтипы и наследование к поддерживаемым формам полиморфизма.

1.6. Предварительное рассмотрение Fun

Fun – это основанный на λ-исчислении язык, расширяющий первостепенное типизированное λ-исчисление второстепенными возможностями, рассчитанными на моделирование полиморфизма и объектно-ориентированных языков.

В разделе 2 рассматривается нетипизированное и типизированное λ-исчисления и разрабатываются базовые элементы для подъязыка выражения типов в Fun. В Fun поддерживаются базовые типы bool, int, real, string и сложные типы для организации записей, функций, рекурсивных типов. Этот набор первостепенных типов (first-order types), как показано далее, используется в качестве основы для создания (с помощью вспомогательных возможностей языка) параметрических типов, абстрактных типов данных и наследования типов .

В разделе 3 приведен краткий обзор теоретических моделей типов, связанных с возможностями Fun, особенно моделей, рассматривающих типы как множества значений. Представление типов как множеств позволяет определить параметрический полиморфизм как пересечение множеств соответствующих типов, а полиморфизм наследования – на основе подмножеств соответствующих типов. Абстракции данных могут также быть определены в терминах операций теории множеств (в данном случае объединения) над соответствующими типами.

В разделах 4, 5 и 6 соответственно расширяют первостепенное λ-исчисление кванторами всеобщности для реализации параметризированных типов,  кванторы существования для реализации абстракций данных и ограниченные кванторы для реализации наследования. Синтаксические расширения для подъязыка выражения типов, определенные этими расширениями, можно суммировать следующим образом.

Type ::= ... | QuantifiedType

QuantifiedType ::=

  "A. Type |                    универсальная квантификация

  $A. Type |                    экзистенциальная квантификация

  "AÍType. Type |  $AÍType. Type      ограниченная квантификация

Кванторы всеобщности привносят в λ-исчисление параметризированные типы, которые могут быть конкретизированы подстановкой реальных параметров на место параметров, находящихся под знаком квантора. Типы, которые стоят под знаком квантора всеобщности, являются сами по себе первостепенными типами, и могут служить реальными параметрами в такой подстановке.

Кванторы существования расширяют набор первостепенных возможностей, разрешая скрытое представление абстрактных типов данных. Взаимодействие двух квантификаций (всеобщности и существования) проиллюстрировано в секции 5.3 для случая стека с универсально квантифицированными типами и экзистенциально квантифицированным представлением сокрытия данных.

Fun поддерживает сокрытие информации не только под кванторами существования, но также через структуру let, облегчая сокрытие локальных переменных в теле модуля. Сокрытие при помощи let - это сокрытие первого порядка, поскольку оно включает локальные идентификаторы и ассоциированные с ними значения, тогда как сокрытие с помощью квантора существования – это сокрытие второго порядка, так как включает в себя сокрытие реализации типа. Отношения между этими двумя формами сокрытия показаны в разделе 5.2, где сравнивается сокрытие в теле пакета с сокрытием в private-частях Ада-пакета.

Ограниченная квантификация расширяет λ-исчисление первого порядка, предоставляя явные параметры подтипов. Наследование (т.е. подтипы и супертипы) моделируется явной параметрической конкретизацией супертипов с образованием подтипов, для которых и будут реально выполняться операции. В объектно-ориентированных языках каждый тип – это потенциальный супертип для последовательно определяемых подтипов, и поэтому их следует моделировать как ограниченно квантифицированные типы. Ограниченная квантификация предоставляет механизм для объектно-ориентированного полиморфизма, который излишне громоздок для явного использования, но полезен при объяснении отношений между параметрическим полиморфизмом и полиморфизмом наследования.

В разделе 7 кратко рассматривается проверку типов и наследование типов в Fun. В приложении к ней приведены правила вывода типов.

В разделе 8 приведена иерархическая классификация объектно-ориентированных систем типов. Fun предоставляет наиболее общую систему типов в этой классификации. Рассматривается также связь Fun и менее общих систем ML, Galileo, Amber и других языков с интересными системами типов.

Надеемся, что читателем будет настолько же интересно читать о Fun, насколько интересно было авторам писать об этом.

2. λ-исчисление

2.1 Нетипизированное λ-исчисление

Эволюцию нетипизированной вселенной в типизированную можно продемонстрировать на примере λ-исчисления, исходно разработанного как нетипизированная нотация для исследования сущности функционального применения операторов к операндам. Выражения в λ-исчислении имеют следующий синтаксис (мы будем использовать fun вместо традиционной λ, чтобы провести соответствие между нотациями языков программирования)

e::=x      переменная – это λвыражение

e::=fun(x)e      функциональная абстракция e

e::=e(e)   оператор е применен к операнду е

Функция identity (id) и функция successor (succ) могут быть определены в λ-исчислении следующим образом (с использованием некого «синтаксического сахара», который будет объяснен ниже). Мы используем ключевое слово value, чтобы определить новое имя, связанное со значением или функцией.

Value id = fun(x)x      функция идентификации

Value succ = fun(x)x + 1       функция successor (для integer).

Функция идентификации может быть применена к произвольному λ-выражению и всегда возвращает λ-выражение. Чтобы определить сложение целых чисел в чистом λ-исчислении, мы выбираем представление целых и определяем операцию сложения таким образом, чтобы результатом ее применения к λ-выражениям, представляющим целые числа n и m сложения было λ-выражение, представляющее n + m. Функция successor применима только к λ-выражениям, которые представляют целые числа. Инфиксная нотация х+1 – это упрощение функциональной нотации +(х)(1). Символы 1 и +, приведенные выше, должны рассматриваться как сокращения выражений λ-исчисления для числа 1 и операции сложения.

Правильность целочисленного сложения не требует предположений о том, что происходит, когда λ-выражение, представляющее сложение, применяется к λ-выражениям, которые не представляют целые числа. Однако если мы хотим, чтобы наша нотация имела хорошую проверку ошибок, желательно определить воздействие сложения на аргументы, которые не являются целыми, как ошибку. В типизированных языках программирования это делается с помощью проверки типов, исключающей (при компиляции) возможность операций с объектами неправильных типов.

Эффект проверки типов в λ-исчислении, так же, как и в обычных языках программирования, состоит в том, что большие классы λ-выражений, корректных в нетипизированном λ-исчислении, становятся неправильным. Класс неверно типизированных выражений зависит от используемой системы типов, и, хотя это и нежелательно, может зависеть даже от конкретного алгоритма проверки типов.

Идею λ-выражений, оперирующих функциями с целью создания других функции, можно проиллюстрировать с помощью функции twice, имеющей следующую форму:

value twice = fun(f)fun(y)f(f(y)) - функция twice

Применение функции twice к функции succ порождает λ-выражение, вычисляющее наследника наследника:

twice(succ) → fun(y) succ(succ(y))

twice(fun(x)x+1) → fun(fun(x)x+1)((fun(x)x+1)(y))

Приведенное выше показывает, как появляются типы при специализации нетипизированной нотации, например, λ-исчиления, для реализации определенных видов вычислений, например целочисленной арифметики. В следующем разделе мы введем в λ-исчисление явные типы. Результирующая нотация похожа на функциональную нотацию в традиционных типизированных языках программирования.

2.2 Типизированное λ-исчисление

Типизированное λ-исчисление похоже на λ-исчисление за тем исключением, что каждая переменная, вводимая как связанная переменная, должна быть явно типизирована. Вследствие этого функция successor в типизированном λ-исчислении имеет следующую форму.

value succ = fun (x:int) x+1

Функция twice имеет параметр f с типом Int → int, и может быть записана так:

Value twice = fun(f:int→int) fun (y:int)f(f(y))

Эта нотация приближается к нотации функциональной спецификации в типизированных языках программирования, но пропускает определение результирующего типа. Мы можем определить результирующий тип, используя ключевое слово returns:

Value succ= fun(x:int) (returns int)x +1

Однако тип результата может быть определен по форме тела функции х+1. Для краткости мы будем опускать определения типов результатов. Механизм выведения типов, позволяющий извлечь эту информацию при компиляции, обсуждается ниже.

Объявления типов реализуются с помощью ключевого слова type. Далее в этой статье, имена типов начинаются с большой буквы, тогда как имена функций и значений – с маленькой.

type IntPair = Int * Int

type IntFun  = Int * Int

Синтаксис «тип1 * тип2» означает тип кортеж (tuple), состоящий из двух неименованных элементов. Такое определение типа часто используется в функциональных языках, например, ML. Кортежи могут иметь более двух полей. Они позволяют передавать в функции и возвращать из них множество значений как единый объект. – прим.ред.

В объявлениях типов приводятся имена выражений типов; однако они ни в каком смысле не создают тип. Это также можно сказать, что мы используем структурную эквивалентность типов вместо эквивалентности имен: два типа эквивалентны, когда они имеют одну и ту же структуру, несмотря на имена.

То, что значение v имеет тип Т, записывается как v:T.

(3;4):IntPair

Succ:IntFun

Вводить переменные путем объявления типов в форме vat:T не нужно, так как тип переменной может быть установлен по форме присвоенного значения. Например, то, что IntPair имеет тип IntPair, можно определить по факту, что (3,4) имеют тип Int*Int, который был объявлен как эквивалентный IntPair.

value intPair = (3,4)

Однако если мы хотим указать тип переменной в процессе ее инициализации, это можно сделать при помощи нотации value var:T = value.

value IntPair:IntPair = (3,4)

value succ:Int → Int = fun(x:Int) x + 1

Локальные переменные могут быть объявлены при помощи конструкции let-in, которая вводит новую инициализированную переменную (после let) в локальной области видимости (выражение, следующее за in). Значение конструкции – это значение следующего выражения:

let a=3 in a+1           возвращает 4

Если нужно определить тип, можно также написать:

let a:Int = 3 in a+1

Конструкция let-in может быть определена в терминах базовых fun-выражений.

let a:T = M in N = (fun(a:T)N)(M)

2.3 Базовые типы, структурированные типы и рекурсия

Типизированное λ-исчисление обычно расширяется за счет различных видов базовых и структурированных типов. В качестве базовых типов мы будем использовать:

§         Unit – простейший тип, с единственным элементом ();

§         Bool – с операцией if-then-else;

§         Int – c арифметическими операциями и операциями сравнения;

§         Real – с арифметическими операциями и операциями сравнения;

§         String – конкатенация строк (инфиксная) ^.

На основе этих базовых типов с помощью конструкторов типов могут быть созданы структурированные типы. Конструкторы типов в нашем языке включают в себя функциональное пространство (→, function space, можно понимать как описание функции), Декартово произведение (*), записи (также называемые помеченными декартовыми произведениями) и тип variant (он же помеченная несвязная сумма).

Пара – это элемент типа декартово произведение, то есть:

value p= 3;true : Int*Bool

Операции над парами – это селекторы первого и второго элемента:

fst(p) возвращает 3

snd(p) возвращает true

Запись – это неупорядоченное множество именованных переменных. Ее тип можно определить, указав тип, ассоциированный с каждым из ее полей. Тип запись определяется последовательностью именованных типов, разделенных запятыми и заключенных в фигурные скобки.

Type ARecordType = {a:Int ; b:Bool,c:String }

Запись такого типа может быть создана путем инициализации полей записи значениями требуемых типов. Это записывается как последовательность именованных значений, разделенных запятыми и заключенных в фигурные скобки.

value r: ARecordType = {a=3;b=true;c=”asd”}

Метки должны быть уникальны внутри каждой конкретной записи или типа записи. Единственная операция над записями – это выбор поля, записываемый как обычно, через точку:

r.b возвращает true.

Поскольку функции – это первоклассные значения, записи в общем случае могут иметь члены-функции.

Type FunctionRecordType = {f1:Int → Int : Real → Real }

Value functionRecord = {f1=succ,  f2 = sin }

Тип «запись» может быть определен на основе существующих типов записей с помощью оператора &, конкатенирующего два типа записей.

Type NewFuctionRecordType = FunctionRecordType &

{

  f3:Bool - > Bool

}

Это сокращение используется вместо явной записи трех полей f1, f2, f3. Такая нотация применима только к типам записей, если в записи нет дублирующихся полей.

С помощью объявления let-in структура данных может быть сделана локальной и доступной только для набора функций (private). Записи с членами-функциями – крайне удобный способ сделать это; здесь private-переменная counter совместно используется функциями increment и total:

value counter =

  let counter = ref(0)

    in

    {

      increment = fun(n:Int) count := count + n,

      total = fun() count

    }

counter.increment(3)

counter.total()                    возвращает 3

Этот пример порождает побочные эффекты, главная польза private-переменных – это возможность скрыто их обновлять. Примитив ref возвращает обновляемую ссылку на объект, и возможность присвоения для таких ссылок ограничена. Эта общая форма сокрытия информации, которая позволяет обновлять локальное состояние, используя статическую область видимости для ограничения видимости.

Тип variant также формируется как неупорядоченное множество типов, в данном случае заключенное в квадратные скобки.

type AVariantType = [a: Int, b:Bool, c: String]

Элементами этого типа могут быть Integer a, Boolean b или String c.

value v1=[a=3]

value v2=[b=true]

value v3=[c=”asd”]

Единственная операция, доступная для типа variant – case-выбор. Case-выражение для типа AVariantType имеет следующую форму:

Case variant of

[a=variableof type Int] действие в случае а

[b=variableof type Bool]       действие в случае b

[c=variableof type String]     действие в случае c

где в каждом случае вводится новая переменная и связывается с соответствующим содержимым variant-а. Эта переменная затем может быть использована в соответствующем действии.

Например, ниже приведена функция, которая возвращает строку по определенному элементу типа AVariantType:

value f = fun (x: AVariantType)

 case x of

[a = anInt] "it is an integer"

[b = aBool] "it is a boolean"

[c = aString] "it is the string: " ^ aString

 otherwise "error"

где содержимое variant-объекта х может быть связано с идентификаторами anInt, aBool, aString.

Нетипизированное λ-исчисление позволяет выражать рекурсивные операторы и использовать их для определения рекурсивных функций. Однако все вычисления, которые можно выразить с помощью λ-исчисления, должны завершаться (грубо говоря, тип функции обычно более сложен, чем тип её результата, следовательно, после некоторого числа применений функции мы получим базовый тип; более того, у нас нет незавершенных примитивов). Следовательно, рекурсивные определения вводятся как новая концепция примитивов. Функция факториала может быть выражена так:

rec value fact =

  fun (n:Int) if n=0 then 1 else n * fact(n-1)

Для простоты мы предполагаем, что единственные значения, которые могут быть рекурсивно определены – это функции.

Наконец, мы вводим рекурсивные определения типов. Это позволит нам, например, определять тип целочисленных списков без использования записей или variant-типов.

rec type IntList =

  [

    nil  : Unit,

    cons : { head: Int, tail: IntList }

  ]

Целочисленный список это либо пустой список (записывается как [nil = ()]), либо соединение целого числа и целочисленного списка (представленное как, например, [cons = { head = 3, tail = nil }]).

3. Типы – это множества значений

Какое понятие типа наиболее адекватно, то есть могло бы содержать полиморфизм, абстракцию и параметризацию? В предыдущих секциях мы начали описывать частную систему типов, предоставляя неформальные правила типизации для лингвистических конструкций, которые мы использовали. Этих правил достаточно, чтобы описать систему типов на интуитивном уровне, и могут быть легко формализованы как система вывода типов. Эти правила ясны и самодостаточны, но для их вывода понадобилось изучение семантики типов, предпринятое в [Hindley 69] [Milner 78] [Damas 82] [MacQueen 84a] и [Mitchell 84].

Хотя нам необязательно подробно обсуждать семантическую теорию типов, может оказаться полезным объяснить некоторые базовые понятия. Они, в свою очередь, полезны для понимания правил типизации, и особенно концепции выделения подтипов, которая будет введена позже.

Есть множество V всех значений, содержащее такие простые значения, как integer, структуры данных, например, пары, записи, variant-типы и функции. Это законченный частичный порядок, созданный с помощью техники Скотта [Scott, 76], но в первом приближении его можно рассматривать, как просто большое множество всех возможных вычисляемых типов.

Тип – это множество элементов V. Не все подмножества V являются корректными типами: они должны удовлетворять некоторым техническим требованиям. Подмножества V, удовлетворяющие таким требованиям, называются идеалами (ideals). Все типы в языках программирования в этом смысле являются идеальными, и нам не придется беспокоиться о подмножествах V, которые не являются идеалами.

Следовательно, тип – это идеал, который является множеством значений. Более того, множество всех типов (идеалов) в V, будучи упорядоченным посредством включения множеств, формирует структуру. На вершине этой структуры находится тип Top (множество всех значений, то есть сама V). Основание структуры – это, в сущности, пустое множество (реально - одноэлементное множество, содержащее наименьший элемент V).

Словосочетание «иметь тип», таким образом, можно интерпретировать как членство в соответствующем множестве. Поскольку идеалы в V могут перекрываться, значения могут иметь много типов.

Множество типов любого языка программирования это, в общем, только маленькое подмножество множества всех идеалов в V. Например, любое подмножество целых определяет идеал (и, следовательно, тип), так же, как и множество всех пар с первым элементом, равным 3. Это в целом хорошо, так как позволяет иметь много систем типов в одной среде. Приходится выбирать, какие идеалы считать интересными в контексте конкретного языка.

Конкретная система типов – это коллекция идеалов V, которая обычно определяется заданием языка выражений типов и отображением выражений типов на идеалы. Идеалы в этой коллекции повышены в ранге до типов определенного языка. Например, можно выбрать в качестве системы типов целые, пары целых и функции. Различные языки будут иметь различные системы типов, но все эти системы типов могут быть построены поверх области определения V (при условии, что V достаточно богато), используя ту же технику.

В мономорфных системах типов каждое значение принадлежит максимум одному типу (кроме наименьшего элемента V, который по определению идеала принадлежит всем типам). Поскольку типы – это множества, значение может принадлежать множеству типов. В полиморфной системе типов большие коллекции значений принадлежат многим типам. Есть также серые области преимущественно мономорфных и почти полиморфных систем, так что определения остаются неточными, но важно то, что базовая модель идеалов в V может объяснить все эти степени полиморфизма.

Поскольку типы – это множества, подтипы просто соответствуют подмножествам. Более того, семантическое утверждение «Т1 – это подтип Т2» в структуре типов соответствует математическому условию T1 Í T2. Это, как будет показано ниже, позволяет очень просто интерпретировать поддиапазоны типов и наследование.

Наконец, если принять, что система типов состоит из единственного множества V, мы получим свободную систему типов, где все значения имеют один и тот же тип. Следовательно, мы можем выразить типизированные и нетипизированные языки в одном семантическом домене и сравнить их.

Структура типов содержит куда больше аспектов, чем можно перечислить в любом типизированном языке. В действительности она включает бесчисленное множество особенностей, так как включает все возможные подмножества целых. Цель языка для описания типов – позволить программисту дать имена типам, соответствующим интересующему его поведению. Для этого языки содержат конструкторы типов, включая конструкторы типов-функций (например, тип T = T1 → T2) для создания функционального типа Т из типов Т1 и Т2.Эти конструкторы позволяют создать бесчисленное множество типов из конечного набора примитивных типов. Однако в структуре типов могут существовать полезные типы, которые нельзя определить с помощью этих конструкторов.

В остальных разделах этой статьи будут показаны более мощные конструкторы типов, позволяющие говорить о типах, соответствующих бесконечным объединениям и пересечениям в структуре типов. В частности, универсальная квантификация позволит нам именовать типы, которые являются бесконечными пересечениями в структуре типов, тогда как экзистенциальная квантификация позволит именовать нам типы соответствующие бесконечным объединениям. Причина введения универсальной и экзистенциальной квантификации – важность результирующих типов в повышении выразительности типизированного языка. Хорошо хоть, что эти концепции математически просты, а также что они относятся к хорошо известным математическим конструкциям.

Модель идеалов – это не единственная изучавшаяся модель типов. По сравнению с другими моделями, она, однако, лучше и интуитивнее в объяснении простых и полиморфных типов интуитивным способом, а именно в терминах множеств значений, и позволяет естественным образом определить наследование. Менее удовлетворительно ее в некотором смысле косвенное толкование параметризации типов, так как типы не могут быть значениями, и толкование операторов типов, заставляющее выходить за пределы модели и рассматривать функции на идеалах. Мы выбрали модель идеалов как базовое представление типов, исходя из ее интуитивности, но многое из обсуждаемого можно было бы сделать, и иногда даже лучше, с использованием других моделей.

Идея типов как параметров полно разработана в λ-исчислении второго порядка [Bruce 84]. Денотационная модель λ-исчисления второго порядка (единственно существующая) – это модель ретрактов [Scott 76]. Здесь типы – это не множества объектов, а специальные функции (так называемые ретракты); их можно интерпретировать как определение множеств объектов, но они сами являются объектами. Поскольку типы – это объекты, модель ретрактов лучше описывает явные типизированные параметры, тогда как идеалы лучше описывают неявные типизированные параметры.

4. Универсальная квантификация

4.1. Универсальная квантификация и обобщенные функции

Типизированного λ-исчисления достаточно, чтобы выразить мономорфные функции. Однако оно не в состоянии адекватно моделировать полиморфные функции. Например, оно требует, чтобы функция twice, о которой говорилось выше, была объявлена как Int → Int, в то время как желательно, чтобы эта функция была объявлена полиморфно как a → a, где a – произвольный тип. Сходным образом и функция идентификации может быть определена только для конкретных типов, например, целых: fun(x:Int)x. Мы не можем отразить тот факт, что её форма не зависит ни от какого типа. Мы не можем выразить идею одинаковой функциональной формы для множества типов, и должны явно связывать переменные и значения с определенным типом в момент, когда такое связывание может быть преждевременным.

То, что данная функциональная форма одинакова для всех типов, можно выразить с помощью кванторов всеобщности. В частности, функцию идентификации можно выразить так:

value id = all[a] fun(x:a) x

В этом определении id а – это переменная типа, а all[a] предоставляет абстракцию для а, так что id – это идентификатор для всех типов. Чтобы применить функцию идентификации к аргументу определенного типа, мы должны сперва представить тип как параметр, а затем аргумент данного типа:

id [Int] (3)

(Здесь используется соглашение, что параметр типа заключен в квадратные скобки, а типизированный аргумент – в круглые)

Такие функции, как id, требующие параметр типа прежде, чем они могут быть применены к функциям некоторого типа, мы будем называть обобщенными функциями (generic functions). Id – это обобщенная функция идентификации.

Заметьте, что all – это, как и fun, оператор связывания, требующий сопоставления фактического параметра при применении функции. Однако all[a] служит для связывания типа, тогда как fun(x:a) служит для связывания переменной данного (возможно, обобщенного) типа.

Несмотря на появление типов, нет никаких предпосылок для манипулирования типами как значениями: типы и значения все еще различны, и абстракции типов и применение типов служат только для проверки типов, без влияний на время выполнения. На самом деле мы можем пропустить информацию о типах в квадратных скобках.

value id = fun(x:a) x где a теперь – переменная свободного типа

id(3)

Здесь задача алгоритма проверки типов - распознать, что а – это свободная переменная типа и переопределить первоначальную информацию all[a] и [Int]. Это часть того, что может делать полиморфный механизм проверки типов, похожий на используемый в ML. В действительности ML идет дальше и позволяет программистам опускать даже оставшуюся информацию о типах.

value id = fun(x) x

id(3)

ML имеет механизм выведения типов, который позволяет системе выводить типы как для мономорфных, так и для полиморфных выражений, поэтому определения типов, пропущенные программистом, могут быть введены системой. Преимущество такого подхода в том, что программист может использовать сокращенную запись нетипизированного λ–исчисления, а система может переводить нетипизированный ввод в полностью типизированные выражения. Однако полностью автоматизированных алгоритмов выведения типов для мощных типизированных систем, которые мы собираемся рассмотреть, не существует. Чтобы выяснить, что происходит, и не зависеть от текущего состояния технологий проверки типов, мы всегда будем записывать достаточно информации о типах для того, чтобы сделать задачу проверки типов тривиальной.

Возвращаясь назад к полностью явному языку, давайте расширим нашу нотацию, чтобы можно было явно говорить о полиморфных функциях. Мы определим тип обобщенной функции от произвольного типа "a. a → a :

type GenericId = "a. a → a

id: GenericId

Вот пример функции, принимающей параметр универсально квантифицированного типа. Функция inst принимает функцию, указанную выше, и возвращает два её экземпляра, для Integer и Boolean:

value inst = fun(f: "a. a → a) (f[Int],f[Bool])

value intid = fst(inst(id)) : Int → Int

value boolid = snd(inst(id)) : Bool → Bool

В общем случае параметры функции, стоящие под знаком квантора всеобщности, наиболее полезны при использовании в разных типах в теле одной функции, например функция вычисления длины списка передается в качестве параметра и используется для списков разного типа.

Чтобы показать некоторую свободу определения полиморфных функций, напишем две версии twice, различающиеся способом передачи параметров. Первая версия, twice1, имеет функциональный параметр f универсального типа. Определение

un(f: "a. a → a) body-of-function

определяет тип функционального параметра f как обобщенный тип, принимает функции любого типа и возвращает значения этого же типа. Экземпляры f в теле twice1 должны иметь формальный параметр типа f[t] и требуют, чтобы при применении функции twice1 был предоставлен фактический тип. Полное определение twice1 требует связывания параметра-типа t как универсально квантифицированного типа и привязки x к t.

value twice1 = all[t] fun(f: "a. a → a) fun(x: t) f[t](f[t](x))

Таким образом, twice1 имеет три связанные переменные, для которых фактические параметры должны быть предоставлены при применении функции.

all[t]           требует фактический параметр-тип

fun(f: "a. a   a) требует функцию типа "a. a a

f(x:t)           требует аргумента, подставляемого вместо типа t.

Применение функции twice1 к типу Int, функция Id и аргумент 3 указываются так:

twice1[Int](id)(3)

Заметьте, что третий аргумент 3 имеет тип Int первого аргумента, и что второй аргумент Id – универсально квантифицированный тип. Заметьте также, что twice1[Int](succ) не будет правильным, так как тип succ – не "a. a → a.

Приведенная ниже функция twice2 отличается от twice1 типом аргумента f, который не универсально квантифицирован. Теперь нам не нужно применять f[t] в теле twice:

value twice2 = all[t] fun(f: t → t) fun(x: t) f(f(x))

twice2[Int]             дает fun(f: Int → Int) fun(x: Int) f(f(x))

Теперь можно посчитать twice как succ.

twice2[Int](succ)       дает fun(x: Int) succ(succ(x))

twice2[Int](succ)(3)    дает 5

Поэтому twice2 сперва принимает параметр-тип Int, который служит для конкретизации функции f: Int → Int, потом получает функцию succ этого типа, и потом принимает элемент типа Int, к которому функция succ применяется дважды.

Дополнительное указание типа требуется для twice2 id, который должен быть сперва конкретизирован в Int:

twice2[Int](id[Int])(3)

Заметьте, что как λ-абстракция (функциональная абстракция), так и универсальная квантификация (абстракция обобщенных типов) – это операторы связывания, требуют замещения формальных параметров действительными параметрами. Разделение типов и значений достигается за счет различных операций связывания типов и значений, а также употреблением различных скобок при указании фактических параметров.

Расширение λ-исчисления для поддержки двух разных механизмов связывания, одиного – для типов, а другого – для значений, полезно при моделировании параметрического полиморфизма и математически интересны при обобщении λ-исчисления для моделирования двух качественно разных абстракций в одной математической модели. В следующих разделах будет введен еще и третий вид абстракции и соответствующие механизмы связывания, но сперва необходимо ввести понятие параметрического типа.

В Fun типы и значения строго отличаются (значения – это объекты, а типы – это множества); следовательно, нужны два разных механизма связывания: fun и all. В некоторых моделях типизации, где типы являются значениями, эти два вида связывания можно объединить, достигая некоторой экономии концепций, но это унификация не вписывается в нашу семантику. В таких моделях параметрический механизм связывания типов, описанный в следующем разделе, можно объединить с fun и all.

4.2. Параметрические типы

Если имеются два определения типов с похожей структурой, например:

type BoolPair = Bool * Bool

type IntPair = Int * Int

может возникнуть желание вынести общую структуру в отдельное параметрическое определение и использовать параметрический тип в определениях других типов:

type Pair[T] = T * T

type PairOfBool = Pair[Bool]

type PairOfInt = Pair[Int]

Объявление типа просто вводит новое имя для выражения типа, и оно эквивалентно выражению этого типа в любом контексте. Объявление типа не вводит нового типа. Следовательно, 3,4 – это IntPair, так как оно имеет тип Int*Int, который является определением IntPair.

Определение параметрического типа вводит новый оператор типа. Pair вверху – это оператор типа, отображающий любой тип Т на Т*Т. Следовательно, тип Pair[Int] – это Int*Int, и, следовательно, 3,4 имеет тип Pair[Int].

Операторы типов – это не типы; они только оперируют типами. В частности, не следует путать следующие нотации:

type A[T] = T → T

type B = " T. T → T

Здесь А – это оператор типа, который при применении к типу Т дает функциональный тип T → T, а В – это тип функции идентификации, который никогда не применяется к типам.

Операторы типов можно использовать в рекурсивных определениях, как в следующем определении обобщенных списков. Заметьте, что List[Item] нельзя считать сокращением, которое должно быть расширено с помощью макросов для получения нормального определения (это вызвало бы бесконечное расширение). Скорее, List лучше считать новым оператором типа, который определен рекурсивно и который отображает некоторый тип на список этого типа.

rec type List[Item] =

  [nil: Unit,

    cons: {head: Item, tail: List[Item]}

  ]

Пустой обобщенный список можно определить и затем конкретизировать так:

value nil = all Item. [nil = ()]

value intNil = nil[Int]

value boolNil = nil[Bool]

Сейчас тип [nil=()] – List[Item] для любого Item (соответствующего определению List[Item]). Следовательно, типы обобщенного nil и его специализаций:

nil : "Item. List[Item]

intNil : List[Int]

boolNil : List[Bool]

Сходным образом можно определить обобщенную функцию cons и другие операции над списками.

value cons : "Item. (Item * List[Item]) → List[Item] =

  all Item.

    fun (h: Item, t: List[Item])

      [cons = {head = h, tail = t}]

Заметьте, что cons может строить только однородные списки, так как его аргументы и результат относятся к одному типу Item.

Следует упомянуть, что в целом существуют проблемы при решении, когда два определения параметрических рекурсивных функций представляют один и тот же тип. [Solomon 78] описывает проблему и ее приемлемое решение, которое включает ограничение формы определений параметрических типов.

5. Квантор существования (экзистенциальная квантификация)

Определение типов для переменных универсально квантифицированного типа имеет следующую форму для любого типа выражения t(a):

p: "a. t(a) (т.е. id: "a. a   a)

По аналогии с универсальной квантификацией можно попробовать определить смысл экзистенциальной квантификации. В общем, для любого выражения типа t(a):

p : $a. t(a)

имеет свойство:

для некоторого типа а, р имеет тип t(a)

Например:

(3,4): $a. a * a

(3,4): $a. a

где а = Int в первом случае, и а=Int*Int – во втором.

Таким образом, мы видим, что данная константа, такая, как (3,4), может удовлетворять многим экзистенциальным типам (предупреждение: в дидактических целях мы здесь присваиваем экзистенциальные типы обычным значениям, например (3,4); это концептуально корректно, но в последующих разделах это будет запрещено в целях реализации проверки типов, и мы потребуем использования конкретных конструкторов для получения объектов экзистенциальных типов.)

Каждое значение имеет тип $a. a, так как для каждого значения существует соответствующий ему тип. Таким образом, тип $a. a определяет множество всех значений, которое мы иногда будем называть Top (наибольший тип):

type Top = $a. a      тип любого значения

Множество всех упорядоченных пар может быть описано следующим экзистенциальным типом.

$a. $b. a *  b   тип любой пары.

Тип любого объекта вместе с применимой к нему целочисленной операцией может быть описан следующим экзистенциальным типом:

$a. a * (a Int)

Пара (3,succ) имеет этот тип, если считать, что а=Int. Аналогично пара ([1,2,3],length) имеет этот тип, если а=List[Int].

Поскольку в набор типов входят не только простые типы, но и универсальные типы, и тип Top, некоторые свойства экзистенциально квантифицированных типов могут сперва показаться не интуитивными. Тип $a. a * a – это не просто тип пар одинаковых типов, как можно было бы ожидать. В действительности даже тип 3,true принадлежит к этому типу. Мы знаем, что 3 и true имеют тип Top; следовательно, есть такой тип а=Top, что 3,true: a * a. Поэтому тип $a. a a – это тип всех пар, так же, как $a. $b. a b. Аналогично, любая функция имеет тип $a. a a, если принять, что а = Top.

Однако $a. a (a Int) порождает связь между типом объекта и типом ассоциированной целочисленной функции. Например (3,length) не принадлежит к этому типу (если считать, что 3 имеет тип Top, надо показать, что length имеет тип Top → Int, но мы знаем только то, что length: "a. List[a] a отображает на integer целочисленные списки, и не можем предположить, что на Integer можно отобразить произвольный объект типа Top).

Не все экзистенциальные типы могут быть полезными. Например, если у нас есть (неизвестный) объект типа $a. a, то у нас нет способов манипулирования им (кроме как передать его еще куда-нибудь), так как у нас нет информации о нем. В случае (неизвестного) объекта типа $a. a * a можно предположить, что это пара, и применить к ней fst и snd, но на том все и кончится, так как информации об а у нас нет.

Экзистенциально типизированные объекты могут, однако, пригодиться, если они в достаточной мере структурированы. Например, x : $a. a * (a → Int) предоставляет достаточную структурированность, чтобы использовать его в вычислениях. Мы можем выполнить:

(snd(x)) (fst(x))

и получить integer.

Следовательно, есть полезные экзистенциальные типы, которые могут скрывать структуру представляемого ими объекта, но показываемой ими структуры достаточно, чтобы позволить манипулировать этими объектами через операции, которые предоставляют сами объекты.

Эти экзистенциальные типы можно использовать, например, при формировании предположительно однородных списков:

[(3,succ); ([1;2;3],length)] : List[$a. a * (a Int)]

Мы можем позже взять некий элемент этого списка и манипулировать им, хотя можем и не знать, какой конкретно элемент мы используем, и какого он типа. Конечно, мы можем формировать разнородные списки типа List[$a. a], но это бесполезное занятие.

5.1 Экзистенциальная квантификация и сокрытие информации

Реальная польза экзистенциальных типов становится очевидна, только тогда когда мы понимаем, что $a. a * (a Int) – это простой пример абстрактного типа, упакованного вместе с его набором операций. Переменная а сама является абстрактным типом, скрывающим представление. В предыдущем примере были приведены представления Int и List[Int]. В этом случае a * (a → Int) – это множество операторов над абстрактным типом: константа типа а и оператор типа a → Int. Эти операторы не именованы, но можно ввести именованные версии, используя тип запись вместо декартова произведения:

x: $a. {const: a, op: a Int}

x.op(x.const)

Поскольку реальное представление а неизвестно (известно только, что оно есть), то мы не можем ничего предположить о нем, и пользователи х не смогут использовать преимущества какой-либо конкретной реализации типа а.

Как уже говорилось, мы были несколько либеральны, применяя разные операторы напрямую к объектам экзистенциальных типов (как x.op above).

С этого момента такое будет запрещено с единственной целью – упростить проверку типов в нашей формальной системе. Вместо этого мы будем использовать явные конструкции языка для создания объектов экзистенциальных типов и манипулирования ими, так же, как использовали абстракции типов all[t] и применение типов exp[t] при создании и использовании объектов универсальных типов.

Обычный объект (3,succ) может быть сконвертирован в абстрактный объект типа $a. a (aInt) при помощи его упаковки (packaging), скрывающей часть его структуры. Операция pack инкапсулирует объект (3,succ) так, чтобы пользователь знал только, что объект типа a (aInt) существует, без знания фактического объекта. Естественно подумать о результирующем объекте как об имеющем экзистенциальный тип $a. a (aInt).

value p = pack [a=Int in a * (a Int)] (3,succ) : $a. a * (a Int)

Такие упакованные объекты, как р, называют пакетами (packages). Значение (3,succ) – это содержимое пакета. Тип a (aInt) – это интерфейс: он определяет структуру содержимого и соответствует спецификации абстракции данных. Связывание а=Int – это представление типов: оно связывает абстрактный тип данных с конкретным представлением (Int) и соответствует скрытому типу данных, ассоциированному с абстракцией данных.

Общая форма операции pack такова:

pack [a = typerep in interface] (contents)

Операция pack – это единственный механизм создания объектов экзистенциального типа. Таким образом, если переменная экзистенциального типа была объявлена так:

p : $a. a * (a Int)

то р может принимать только значения, созданные операцией pack.

Перед использованием пакет нужно открыть:

open p as x in (snd(x))(fst(x))

Открытие пакета вводит имя х для содержимого пакета, которое можно использовать в области видимости, следующей после in. Если структура х определена именованными членами, к членам открытого пакета можно обращаться по имени:

value p = pack [a = Int in {arg:a, op:a Int}] (3, succ)

open p as x in x.op(x.arg)

Может понадобиться ссылаться на (неизвестный) тип, скрытый пакетом. Например, предположим, что нам нужно применить второй член p к значению абстрактного типа, предоставленного как внешний аргумент. В этом случае на неизвестный тип b должна быть явная ссылка. Можно использовать такую форму:

open p as x [b] in ... fun(y:b) (snd(x))(y) ...

Здесь имя типа b ассоциируется со скрытым представлением типа в области видимости, следующей за in. Тип выражения, следующего за in, не должен содержать b, чтобы b не вышло из своей области видимости.

Функция open в основном служит для связывания имен с представлениями типов и помогает механизму проверки типов при проверке ограничений. Во многих ситуациях может придти мысль сократить «open p as x in x.a» до «p.a». Такие сокращения лучше не применять во избежание путаницы, но они вполне применимы.

И pack, и open во время исполнения не влияют на данные. При достаточно умном механизме проверки типов можно опустить эти конструкции и вернуться к нотации, использованной в предыдущих разделах.

5.2 Пакеты и абстрактные типы данных

Чтобы проиллюстрировать применимость нашей нотации к реальным языкам программирования, мы покажем, как записи с функциональными полями могут быть использованы для моделирования пакетов Ада и как экзистенциальная квантификация может быть использована для моделирования абстракций данных в Ада [D.O.D. 83]. Рассмотрим тип Point1, вводящий операции для создания геометрических точек (глобально определенного типа Point) из пар действительных чисел и для получения координат:

type Point = Real * Real

type Point1 =

  {

    makepoint: (Real * Real) Point,

    x_coord: Point Real,

    y_coord: Point Real

  }

Значения типа Point1 могут быть созданы с помощью инициализации каждого имени функций типа Point1 функциями требуемого типа.

value point1 : Point1 =

  {

    makepoint = fun(x:Real,y:Real) (x,y),

    x_coord = fun(p:Point) fst(p),

    y_coord = fun(p:Point) snd(p)

  }

В Ада пакет point1 с функциями makepoint, x_coord и y_coord может быть определен так:

package point1 is

function makepoint (x:Real, y:Real) return Point;

function x_coord (P:Point) return Real;

function y_coord (P:Point) return Real;

end point1;

Определение пакета – это не определение типа, а часть определения значения. Чтобы завершить определение значения в Ада, нужно представить тело пакета в следующей форме:

package body point1 is

  function makepoint (x:Real, y:Real) return Point;

    -- реализация makepoint

  function x_coord (P:Point) return Real;

    -- реализация x_coord

  function y_coord (P:Point) return Real;

    -- реализация y_coord

end point1;

Тело пакета предоставляет тело функций для функциональных типов в определении пакета. В противоположность нашей нотации, которая позволяет, чтобы разные тела функций соответствовали разным значениям типов, Ада не позволяет, чтобы пакеты имели типы, и напрямую определяет тело функции для каждого типа функции в теле пакета.

Пакеты позволяют определять группы связанных функций, совместно использующих локальные скрытые структуры данных. Например, пакет localpoint с локальной структурой данных point имеет следующую форму:

Package body localpoint is

  -- разделяемая глобальная переменная функций marketpoint, x_coord, y_coord

  Point: Point ;

  procedure makepoint(x,y: Real); ...

  function x_coord return Real; ...

  function y_coord return Real; ...

end localpoint;

В нашей нотации скрытые локальные переменные могут быть реализованы при помощи конструкции let:

value localpoint =

  let p: Point = ref((0,0))

  in

  {

    makepoint = fun(x: Real, y: Real) p := (x, y),

    x_coord = fun() fst(p),

    y_coord = fun() snd(p)

  }

Хотя в Ада нет концепции типа пакета, в ней есть понятие шаблона пакета, который имеет некоторые, хотя и не все, свойства типа. Шаблоны пакетов вводятся ключевым словом generic:

generic

  package Point1 is

    function makepoint (x:Real, y:Real) return Point;

    function x_coord (P:Point) return Real;

    function y_coord (P:Point) return Real;

  end Point1;

Значения point1 и point2 шаблона обобщенного пакета Point1 могут быть введены как:

package point1 is new Point1;

package point2 is new Point1;

Все значения пакетов, соответствующих данному шаблону обобщенного пакета, имеют одно и тоже тело пакета. Определение пакета в Ада до исполнения статически ассоциировано с его телом, тогда как типизированные значения типов записей при выполнении команды создания значений динамически ассоциируются с телами функций.

К членам пакетов, созданных по обобщенному пакету, можно обращаться, используя нотацию записей.

type p is Point;

p = point1.makepoint(3,4);

Таким образом, пакеты похожи на значения записей в том, что разрешает обращаться к своим членам с помощью той же нотации, что и при выборе членов записи. Но пакеты в Ада – это не первокласные сущности. Они не могут передаваться как параметры процедур, не могут быть членами массивов или записей, и не могут использоваться как значения переменных. Более того, шаблоны обобщенных пакетов – это не типы, хотя и похожи на них в том, что позволяют создавать экземпляры. На самом деле в Ада есть два похожих, но несколько различающихся механизма для управления структурами, похожими на записи, один – для работы с записями некоторого типа, а другой – для работы с пакетами, с которыми ассоциированы обобщенные шаблоны. Сопоставляя два механизма Ада (для типов записи и обобщенных пакетов) с единым механизмом в нашей нотации, мы получаем оценку и понимание преимуществ единого расширения типов до записей с функциями-членами.

Пакеты в Ада, которые просто инкапсулируют множество операций для открыто определенного типа данных, не нуждаются в причудливых операторах типа. Они могут быть смоделированы в нашей нотации с помощью простого типизированного λ-исчисления без кванторов существования. И только если нам потребуется спрятать представление типа, используя private-типы, понадобятся кванторы существования.

Конструкция let в предыдущем примере использовалась для реализации сокрытия информации. Мы называем это сокрытием информации первого порядка, так как оно достигается за счет ограничения области видимости на уровне значений. Это можно сравнить с сокрытием информации второго порядка, которое реализуется с помощью кванторов существования, которые ограничивают область видимости на уровне типов.

В Ада пакет point2 с private-типом Point может быть определен так:

package point2

  type Point is private;

  function makepoint (x:Real, y:Real) return Point;

  function x_coord (P:Point) return Real;

  function y_coord (P:Point) return Real;

  private

    -- скрытое локальное определение типа Point

end point2;

Private-тип Point можно смоделировать при помощи кванторов существования.

type Point2 =

  $Point.

  {

    makepoint: (Real Real) Point,

    x_coord: Point Real,

    y_coord: Point Real

  }

Иногда удобно представлять определение экзистенциально квантифицированного типа как параметрическую функцию от скрытого параметра типа. В данном примере Point2WRT[Point] можно определить так:

type Point2WRT[Point] =

  {

    makepoint: (Real * Real)   Point,

    x_coord: Point Real,

    y_coord: Point Real

  }

Нотация WRT в Point2WRT должна читаться как «with respect to», подчеркивая тот факт, что это определение типов соотносится с параметром типа.

Значение point2 экзистенциального типа Point2 можно создать с помощью операции pack.

value point2 : Point2 = pack [Point = (Real * Real) in Point2WRT[Point]]

  point1

Операция pack скрывает представление Real*Real типа Point, имеет экзистенциально параметризируемый тип Point2WRT[Point] как часть своего определения и предоставляет как свое скрытое тело определенное ранее значение point1, реализующее операции для этого представления данных.

Заметьте, что Point2WRT[Point] представляет параметризированное выражение типа, которое, будучи предоставленным с фактическим параметром типа, например, Real, определяет тип (в данном случае тип записи с тремя членами). Отношения между этим и другими видами параметризации, описанными к этому моменту, показаны ниже:

Функциональная абстракция: fun(x:type) value-expr(x). Параметр х – это значение, а результат подстановки фактического параметра вместо формального определяет значение.

Квантификация: all(a) value-expr(a). Параметр а – это тип, и результат подстановки фактического параметра вместо формального определяет значение.

Абстракция типов. TypeWRT[T] = type-expr(T). Параметр Т – это тип, результат подстановки фактического параметра вместо формального тоже тип.

Формальные параметры должны быть типами, тогда как фактические могут быть произвольно сложными значениями. Однако расширение класса именованных типов до включения экзистенциально квантифицируемых типов расширяет и набор аргументов, которые можно подставлять вместо формальных параметров.

Экзистенциальная квантификация может быть использована для моделирования private-типов в Ада. Однако, как показано в следующих примерах, они более общие, чем средства абстракции данных в Ада.

5.3 Объединение универсальной и экзистенциальной квантификации

В этом разделе приведен пример, демонстрирующий взаимодействие между экзистенциальной и универсальной квантификацией. Универсальная квантификация возвращает обобщенные типы, тогда как экзистенциальная – абстрактные типы данных. Комбинация этих нотаций даст нам параметрическую абстракцию данных.

Стеки – идеальный пример взаимодействия шаблонных типов и абстракций данных. Простейшая форма стека имеет как специфический тип элемента, такой, как integer, и специфичную реализацию структуры данных, такую, как список или массив. Обобщенные стеки параметризируют тип элемента, а абстракция от представления данных может быть выполнена с помощью создания пакета, имеющего экзистенциальный тип данных. Стек с параметризованным типом элементов и скрытое представление данных реализуются при помощи комбинации универсальной квантификации для реализации параметризации и экзистенциальной квантификации для реализации абстракций данных.

Далее будут использованы следующие операции над списками и массивами.

nil: "a. List[a]

cons: "a. (a * List[a]) List[a]

hd: "a. List[a] a

tl: "a. List[a] List[a]

null: "a. List[a] Bool

array: "a. Int Array[a]

index: "a. (Array[a] * Int) a

update: "a. (Array[a] * Int * a) Unit

Начнем с конкретного типа IntListStack c целочисленными элементами и списковым представлением данных. Этот конкретный тип может быть реализован как кортеж операций без всякой квантификации.

 type IntListStack =

  {

    emptyStack: List[Int],

    push: (Int * List[Int]) List[Int],

    pop: List[Int] List[Int],

    top: List[Int] Int

  }

Экземпляр этого типа стека с членами, инициализированными как специфические функциональные значения можно определить так:

value intListStack : IntListStack =

  {

    emptyStack = nil[Int],

    push = fun(item : Int, stack : List[Int]) cons[Int](item, stack),

    pop  = fun(stack : List[Int]) tl[Int](stack),

    top  = fun(stack : List[Int]) hd[Int](stack)

  }

Может существовать стек целых чисел, реализованный в виде пар, включающих массив и индекс в этом массиве от верха стека; этот конкретный тип опять же может быть реализован как кортеж без какой-либо квантификации.

type IntArrayStack =

  {

    emptyStack: (Array[Int] * Int),

    push: (Int * (Array[Int] * Int)) (Array[Int] * Int),

    pop: (Array[Int] * Int) (Array[Int] * Int),

    top: (Array[Int] * Int) Int

}

Экземпляр IntArrayStack – это экземпляр типа кортежа с полями операций, инициализированными операциями представления стека в виде массива.

value intArrayStack : IntArrayStack =

  {

    emptyStack = (Array[Int](100),-1),

    push = fun(item : Int, stack : (Array[Int] * Int))

      update[Int](fst(stack), snd(stack) + 1, item); (fst(stack), snd(stack) + 1),

    pop = fun(stack : (Array[Int] * Int)) (fst(stack), snd(stack) - 1),

    top = fun(stack : (Array[Int] * Int)) index[Int](fst(stack), snd(stack))

  }

Приведенные выше стеки можно обобщить, либо сделав тип элементов обобщенным, либо скрыв представление данных стека. Следующий пример показывает, как можно реализовать обобщенный тип с помощью универсальной квантификации. Сперва мы определим тип GenericListStack как универсально квантифицируемый тип:

type GenericListStack =

  " Item.

  {

    emptyStack: List[Item],

    push: (Item * List[Item]) → List[Item],

    pop: List[Item] → List[Item],

    top: List[Item] → Item

  }

Экземпляр этого универсального типа может быть создан при помощи универсальной квантификации экземпляра записи, чьи поля инициализированы операциями, параметризированными обобщенным универсально квантифицированным параметром.

value genericListStack : GenericListStack =

  all[Item]

  {

    emptyStack = nil[Item],

    push = fun(item:Item, stack:List[Item]) cons[Item](item, stack),

    pop = fun(stack:List[Item]) tl[Item](stack),

    top = fun(stack : List[Item]) hd[Item](stack)

  }

genericListStack имеет, как и предполагает его имя, конкретную списковую реализацию структуры данных стека. Аналогично можно определить альтернативный тип GenericArrayStack с конкретной реализацией в виде массива:

type GenericArrayStack = ...

value genericArrayStack : GenericArrayStack = ...

Так как представление данных стека не важно для пользователя, лучше спрячем его, чтобы интерфейс стека не зависел от скрытого представления данных. Мы будем использовать единственный тип GenericStack, который реализован как обобщенный стек, реализованный на базе списка, или обобщенный стек, реализованный на базе массива. Пользователи GenericStack не должны знать, какую реализацию GenericStack они используют.

Вот здесь нам нужны экзистенциальные типы. Для любого типа элемента должна существовать реализация стека, предоставляющая операции над стеком. Это реализуется в типе GenericStack, определенном в терминах универсально квантифицированного параметра Item и экзистенциально квантифицированного параметра Stack:

type GenericStack =

  "Item. $Stack. GenericStackWRT[Item][Stack]

Тип GenericStackWRT[Item][Stack] с двумя параметрами может быть в свою очередь определен как кортеж двойных параметризированых операций.

type GenericStackWRT[Item][Stack] =

  {

    emptystack: Stack,

    push: (Item, Stack) → Stack,

    pop: Stack → Stack,

    top: Stack → Item

  }

Заметьте, что в этом определении нет ничего, позволяющего различать роли параметров Item и Stack. Однако в определении GenericStack параметр Item универсально квантифицирован, показывая, что он представляет скрытый абстрактный тип данных.

Теперь мы можем абстрагировать пакеты genericListStack и genericArrayStack в пакеты типа GenericStack:

value listStackPackage : GenericStack =

  all[Item]

    pack[Stack = List[Item] in GenericStackWRT[Item][Stack]]

      genericListStack[Item]

value arrayStackPackage : GenericStack =

  all[Item]

    pack[Stack = (Array[Item] * Item) in GenericStackWRT[Item][Stack]]

      genericArrayStack[Item]

И listStackPackage, и arrayListPackage имеют один и тот же тип и отличаются только формой представления скрытых данных. Более того, такие функции, как следующая useStack, могут работать, ничего не зная о реализации:

value useStack =

  fun(stackPackage: GenericStack)

    open stackPackage[Int] as p [stackRep]

    in p.top(p.push(3,p.emptystack));

и могут принимать любую реализацию GenericStack в качестве параметра:

useStack(listStackPackage)

useStack(arrayStackPackage)

В определении GenericStack тип Stack почти никак не связан с Item, а мы хотим, чтобы, независимо от реализации Stack, стеки были коллекциями элементов (на самом деле существует слабая зависимость Stack от Item, обусловленная порядком следования кванторов). Из-за этого можно создавать объекты типа GenericStack, где стеки не имеют ничего общего с элементами и не подчиняются таким свойствам как: pop(push(item, stack)) = item. Это ограничение исправлено в более мощных системах, например, [MacQueen 86] и [Burstall 84], где можно делать абстрактными операторы типов (например, List) вместо самих типов (т.е. List[Int]), и можно напрямую выражать, что представление Stack должно быть основано на Item (но даже в таких более выразительных системах типов можно создать пакеты стека, не удовлетворяющие свойствам стека).

5.4 Квантификация и модули

Теперь мы готовы к главному примеру: геометрическим точкам. Введем абстрактный тип с операциями mkpoint (создающей новую точку по двум действительным числам), x-coord и y-coord (возвращающими x- и у-координаты точки):

type Point =

  $PointRep.

  {

    mkpoint: (Real * Real) → PointRep,

    x-coord: PointRep → Real,

    y-coord: PointRep → Real

  }

Наша цель – определить значения этого типа, которые скрывают и представление PointRep, и реализацию операций mkpoint, x-coord и y-coord относительно этого преставления. Для этого мы определим тип этих операций как параметрические типы с представлением точки PointRep в качестве параметра. Имя типа PointWRT подчеркивает, что операции определены по отношению к конкреиному представлению, и наоборот, абстрактный тип Point не зависит от представления.

type PointWRT[PointRep] =

  {

    mkpoint: (Real * Real) → PointRep,

    x-coord: PointRep → Real,

    y-coord: PointRep → Real

}

Экзистенциальный тип Point может быть определен на основе PointWRT при помощи экзистенциальной абстракции относительно PointRep.

type Point = $PointRep. PointWRT[PointRep]

Связь между операциями, зависящими от представлений, и соответствующими абстрактными типами данных становится более понятной на примере процесса абстракции для некоторых специфичных представлений точек. Определим пакет декартовой точки, в котором представление точки – это пара действительных чисел, а операции над ними, mkpoint, x-coord и y-coord, выглядят так:

value cartesianPointOps =

  {

    mkpoint = fun (x:Real, y:Real) (x,y),

    x-coord = fun (p: Real * Real) fst(p),

    y-coord = fun (p: Real * Real) snd(p)

  }

Пакет с представлением точки Real * Real, содержащий приведенные выше реализации операций над точками, может быть определен следующим образом:

value cartesianPointPackage =

  pack [PointRep = Real * Real in PointWRT[PointRep]]

    cartesianPointOps

Сходным образом можно определить пакет полярных точек, с таким же представлением Real * Real, что и у декартовых точек, но с другим (в полярных координатах) представлением операций:

value polarPointPackage =

  pack[PointRep = Real * Real in PointWRT[PointRep]]

    {

      mkpoint = fun (x : Real, y : Real) ... ,

      x-coord = fun (p : Real * Real) ... ,

      y-coord = fun (p : Real * Real) ...

    }

Эти примеры показывают, как пакеты реализуют абстракции данных путем сокрытия представления данных и реализации операторов. Пакеты декартовых и полярных точек имеют один и тот же экзистенциальный тип Point, используют один и тот же параметрический тип PointWRT[PointRep] для определения структуры операций над точками и имеют один и тот же тип представления данных Real * Real. Они отличаются только содержанием пакета, определяющего реализацию функции. В общем, данный экзистенциальный тип заставляет все пакеты такого типа иметь одинаковую структуру операций. Но и типы представления внутренних данных, и значения (реализации) операций у разных реализаций абстрактных типов данных могут отличаться.

Абстрактный тип данных, упакованный со своими операторами, как Point - это, кроме всего прочего, простой пример модуля. В общем случае модули могут импортировать другие (известные) модули, или могут быть параметризованными относительно других (в том числе неизвестных) модулей.

Параметрические модули можно рассматривать как функции над экзистенциальными типами. Здесь приведен пример расширения пакета Point еще одной операцией add. Вместо расширения конкретного пакета Point мы напишем процедуру для расширения любого пакета Point с неизвестным представлением Point. Вспомните, что & – это оператор конкатенации типа запись:

type ExtendedPointWRT[PointRep] =

  PointWRT[PointRep] & { add : (PointRep * PointRep) → PointRep }

type ExtendedPoint = $PointRep. ExtendedPointWRT[PointRep]

value extendPointPackage =

  fun (pointPackage: Point)

    open pointPackage as p [PointRep] in

      pack[PointRep' = PointRep in ExtendedPointWRT[PointRep']]

        p &

        {

          add = fun (a:PointRep, b:PointRep)

            p.mkpoint(p.x-coord(a)+p.x-coord(b),

            p.y-coord(a)+p.x-coord(b))

        }

value extendedCartesianPointPackage =

  extendPointPackage(cartesianPointPackage)

value extendedPolarPointPackage =

  extendPointPackage(polarPointPackage)

Вернемся к модулю Point и покажем, как можно на его основе построить другие модули. В частности, построим на основе модуля Point модули Circle и Rectangle, а затем определим модуль Picture, использующий Circle и Rectagle. Поскольку разные экземпляры Point могут быть основаны на разных представлениях данных, если мы хотим добиться взаимодействия Circle and Rectangle, необходимо удостовериться, что круги и прямоугольники основаны на одинаковых представлениях Point.

Пакет Circle предоставляет операции для создания круга из точки (центр) и действительного числа (радиус), а также операции, которые возвращают центр и радиус круга. Определена также операция diff (расстояние между центрами двух кругов). Два параметра diff – это круги, основанные на одинаковых реализациях Point. Пакет Circle также предоставляет пакет Point для доступа к операциям над точками, работающим с тем же представлением точки, что и пакет Circle.

type CircleWRT2[CircleRep,PointRep] =

  {

    pointPackage: PointWRT[PointRep],

    mkcircle: (PointRep * Real) CircleRep,

    center: CircleRep PointRep,

    radius: CircleRep Real,

    diff: (CircleRep * CircleRep) Real

  }

type CircleWRT1[PointRep] =

  $CircleRep. CircleWRT2[CircleRep,PointRep]

type Circle = $PointRep. CircleWRT1[PointRep]

type CircleModule =

  "PointRep. PointWRT[PointRep]   CircleWRT1[PointRep]

value circleModule : CircleModule =

  all[PointRep]

    fun (p : PointWRT[PointRep])

      pack[CircleRep = PointRep * Real in CircleWRT2[CircleRep,PointRep]]

      {

        pointPackage = p,

        mkcircle = fun (m : PointRep,r : Real) (m, r),

        center = fun (c : PointRep * Real) fst(c),

        radius = fun (c : PointRep * Real) snd(c),

        diff = fun (c1 : PointRep * Real, c2 : PointRep * Real)

          let p1 = fst(c1)

          and p2 = fst(c2)

          in sqrt((p.x - coord(p1) - p.x - coord(p2)) ** 2

            + (p.y-coord(p1) - p.y-coord(p2)) ** 2)

      }

Теперь мы уже можем создавать конкретные пакеты для круга, применяя circleModule к различным пакетам Point. Мы можем также определять различные версии circleModule для различных представлений круга, и все это можно применять к различным пакетам Point для получения пакетов для кругов. Здесь мы применяем circleModule к cartesianPointPackage и к polarPointPackage для получения пакетов для кругов, построенных с использованием декартовых и полярных точек.

value cartesianCirclePackage =

  open cartesianPointPackage as p [Rep] in

    pack[PointRep = Rep in CircleWRT1[PointRep]]

      circleModule[Rep](p)

value polarCirclePackage =

  open polarPointPackage as p [Rep] in

    pack[PointRep = Rep in CircleWRT1[PointRep]]

      circleModule[Rep](p)

Чтобы использовать пакеты для кругов, их сперва нужно открыть. На самом деле их придется открывать дважды (заметьте, что тип Circle имеет двойную экзистенциальную квантификацию) для связывания PointRep и CircleRep с представлениями точки и круга, используемыми в пакете. Здесь используется сокращенная форма open, эквивалентная двум последовательным открытиям:

open cartesianCirclePackage as c [PointRep] [CircleRep]

in ... c.mkcircle(c.pointPackage.mkpoint(3,4),5) ...

Прямоугольник определяется двумя точками: верхней левой и правой нижней. Определение модуля прямоугольника очень похоже на определение модуля круга. Мы должны удостовериться, что две определяющие прямоугольник точки основаны на одинаковом представлении Point.

type RectWRT2[RectRep,PointRep] =

  {

    pointPackage: PointWRT[PointRep],

    mkrect: (PointRep * PointRep) → RectRep,

    toplft: RectRep → PointRep,

    botrht: RectRep → PointRep

  }

type RectWRT1[PointRep] =

  $RectRep. RectWRT2[RectRep,PointRep]

type Rect = $PointRep. RectWRT1[PointRep]

type RectModule =

  "PointRep. PointWRT[PointRep] → RectWRT1[PointRep]

value rectModule =

  all[PointRep]

    fun (p : PointWRT[PointRep])

      pack[PointRep = PointRep in RectWRT1[PointRep]]

      {

        pointPackage = p,

        mkrect = fun (tl : PointRep, br : PointRep) (tl, br),

        toplft = fun (r : PointRep * PointRep) fst(r),

        botrht = fun (r : PointRep * PointRep) snd(r)

      }

Теперь объединим все это в модуль фигур, использующий круги и прямоугольники (основанные на едином представлении точек), и определяющий операцию boundingRect, возвращающую наименьший прямоугольник, содержащийся в данном круге.

type FiguresWRT3[RectRep,CircleRep,PointRep] =

  {

    circlePackage: CircleWRT[CircleRep,PointRep]

    rectPackage: RectWRT[RectRep,PointRep]

    boundingRect: CircleRep   RectRep

  }

type FiguresWRT1[PointRep] =

  $RectRep. $CircleRep. FigureWRT3[RectRep,CircleRep,PointRep]

type Figures = $PointRep. FigureWRT1[PointRep]

type Figures =

  "PointRep. PointWRT[PointRep]   FiguresWRT1[PointRep]

value figuresModule =

  all[PointRep]

    fun (p : PointWRT[PointRep])

      pack[PointRep = PointRep in FiguresWRT1[PointRep]]

        open circleModule[PointRep](p) as c [CircleRep]

        in open rectModule[PointRep](p) as r [RectRep]

          in

          {

            circlePackage = c,

            rectPackage = r,

            boundingRect = fun(c: CircleRep) ..r.mkrect(..c.center(c)..)..

          }

5.5 Модули – это значения первого класса

В предыдущих разделах показано, что пакеты и модули – это объекты первого класса: это легальные значения, которые могут быть передаваться функциям и возвращаться ими, а также храниться в объектах. Например, можно писать программы, которые, в зависимости от условий, порождают тот или иной пакет одного и того же экзистенциального типа, реализующего интерфейс, и возвращают его для использования при создании больших пакетов.

Можно также выразить и процесс связывания модулей: мы делали это в предыдущем примере, например, cartesianCirclePackage был создан путем связывания cartesianPointPackage и circleModule. Следовательно, процесс создания систем из модулей можно выразить на языке, используемом для создания модулей, и на фазе линковки можно использовать всю мощь языка.

Мы показали, что можем выразить параметрические модули и механизм линковки, но мы не заявляем, что это самая удобная нотация. Наша цель – показать, что все эти концепции могут быть выражены в относительно простой среде. Еще есть, что делать, например, не дать нотации выйти из-под контроля. Наибольшая проблема здесь в том, что при создании нового экземпляра модуля необходимо знать граф зависимостей модулей, и для каждого нового экземпляра приходится выполнять линковку вручную. Эти проблемы подробно разобраны в механизме модулей в ML [MacQueen 84b].

6.Ограниченная квантификация

6.1 Включение типов, поддиапазоны и наследование

Мы говорим, что тип А включен в, или является подтипом другого типа B, если все значения А также являются значениями типа В, то есть если А, рассматриваемый как множество значений – это подмножество В. Это общее определение включения различает правила включения для разных конструкторов типов. В этом разделе мы обсудим включение поддиапазонов, записей, variant-ов и функциональных типов. Включения универсально и экзистенциально квантифицированных типов обсуждается в последующих разделах.

Как вступление к включению типов записей, мы сперва рассмотрим простейшую теорию включений типов поддиапазонов целых. Пусть n..m описывает подтип типа Int, соответствующий поддиапазонам от n до m включительно, где m и n – это произвольные целые числа. Следующие отношения включения справедливы для типов поддиапазонов целых:

n..m ≤ n'..m' iff n' ≤ n and m ≤ m'

   где слева от ≤ включение типа (type inclusion).

Типы-поддиапазоны могут появиться как определения типов в λ-выражениях.

value f = fun (x: 2..5) x + 1

f : 2..5   3..6

f(3)

Константа 3 имеет тип 3..3 и также имеет тип любого супертипа, включая приведенный выше тип x:2..5. Таким образом, это правильный аргумент f. Сходным образом следующее тоже должно быть правильно:

value g = fun (y: 3..4) f(y)

так как тип у – это подтип области определения f. Фактический параметр функции может иметь любой подтип соответствующего формального параметра.

Рассмотрим функцию типа 3..7 → 7..9. Ее можно рассматривать, например, как функцию типа 4..6 → 6..10, так как она отображает целые между 3 и 7 (и следовательно, между 4 и 6) на целые между 7 и 9 (и следовательно, между 6 и 10). Заметьте, что домен сужается, когда как поддомен расширяется. В общем случае мы можем сформулировать правила включения для функций следующим образом:

s → t ≤ s' → t' iff s' ≤ s and t ≤ t'

Заметьте сходство этого правила и правила для поддиапазонов.

В этих правилах включения интересно то, что они также работают для функциональных типов высшего порядка. Например:

value h = fun (f: 3..4 → 2..7) f(3)

Может быть применено к f:

h(f)

благодаря правилам включения. То же рассуждение подходит и для типа «запись». Предположим, у нас есть типы:

type Car = { age : Int, speed : Int, fuel : String }

type Vehicle = { age : Int, speed : Int }

Мы хотим показать, что все автомобили – это транспортные средства, т.е., Car – это подтип Vehicle. Чтобы добиться этого, нам потребуется следующее правило включения для типа «запись»:

{ a₁ : t₁, .. , a_n : t_n, .. , a_m : t_m } ≤ { a₁ : u₁, .. , a_n : u_n }

  iff t_i ≤ u_i for i Î 1..n.

Например, тип-запись А – это подтип другой записи В, если А имеет все атрибуты (поля), которые имеет В (возможно, больше), и типы общих атрибутов связаны отношением подтипов.

Тип Vehicle – это множество всех записей, имеющих, по крайней мере, целочисленное поле Age, целочисленное поле speed и, возможно, какие-то еще. Следовательно, любой автомобиль попадает в это множество, и множество всех машин – это подмножество множества транспорт. Опять же, подтипы – это подмножества.

Выделение подтипов в записях соответствует концепции наследования (подклассов) в языках, особенно если записи могут иметь функциональные члены. Пример класса – это запись с функциями и локальными переменными, а пример подкласса – это запись, по крайней мере, с теми же функциями и переменными, и возможно, с какими-то еще.

На самом деле мы можем выразить даже множественное наследование. Если добавить определения типов:

type Object = { age : Int }

type Machine = { age : Int, fuel : String }

то получится, что Car – это подтип (наследующий свойства) типов Vehicle и machine, а они оба, в свою очередь, являются подтипами типа object. Наследование для записей распространяется также на более высокие функциональные типы, как и в случае поддиапазонов, правило включения для пространства функции тоже поддерживается.

В случае variant-типов правило включения выглядит так:

[a₁ : t₁, .. , a_n : t_n] ≤ [a₁ : u₁, .. , a_n : u_n, .. , a_m : u_m]

  iff t_i ≤ u_i for i Î1..n.

Например, любой яркий цвет – это цвет:

type brightColor = [red : Unit, green : Unit, blue : Unit]

type color = [red : Unit, green : Unit, blue : Unit, gray : Unit, brown : Unit]

и любая функция, работающая с цветами, сможет работать и с яркими цветами.

Более детальные примеры таких видов наследования можно найти в первой части [Cardelli 84b].

6.2 Ограниченная универсальная квантификация и выделение подтипов

Мы подошли к проблеме совместного использования выделения подтипов и параметрического полиморфизма. Полезность раздельного применения этих двух концепций мы уже видели; теперь мы покажем, что иногда полезно и даже необходимо применять их вместе.

Возьмем простейшую функцию:

value f₀ = fun(x: {one: Int}) x.one

которая может быть применена к записям вида {one=3,two=true}. Ее можно сделать полиморфной:

value f = all[a] fun(x: {one: a}) x.one;

f[t] можно использовать с записями вида {one=y} для любого y типа t, и с записями типа {one=y, two=true}.

Нотация all[a]e позволяет отразить то, что переменная типа может принимать любое значение типа, но не позволяет определять переменные типов для подмножеств множества типов. Общее средство для определения переменных, способных принимать значения произвольных подмножеств типов, может быть реализовано с помощью квантификации над множествами типов, определенных указанными предикатами. Но нам не нужна такая степень обобщения, и мы можем удовлетвориться указанием конкретного класса подмножеств – а именно, множества всех подтипов данного вида. Это можно сделать с помощью ограниченной квантификации.

Переменная типа, определенная на множестве всех подтипов типа Т, может быть определена путем ограниченной квантификации:

all[a £ T] e    а определено на всех подтипах Т в области е.

Вот функция, которая принимает любую запись, имеющую целочисленное поле one, и возвращает её содержимое:

value g₀ = all[a £ {one: Int}] fun(x: a) x.one

g₀ [{one: Int, two: Bool}]({one=3, two=true})

Заметьте, что есть небольшое различие между g_o и f_o; все, что мы сделали – это наложили ограничения, что аргумент должен быть подтипом {one:Int} от параметра fun к параметру all. Теперь у нас есть два способа выражения ограничений включения: неявно, через параметры функции, и явно, с помощью ограниченных кванторов. Теперь, благодаря ограниченным кванторам, можно более не использовать другой механизм, требующий строгого сопоставления типов при передаче параметра, но мы оставим его для удобства.

Чтобы выразить тип g₀ нам нужно ввести ограниченные кванторы в выражение типа:

g₀ : "a £ {one: Int}. a   Int

Теперь у нас есть способы выражения как наследования, так и параметрического полиморфизма. Вот новая версия g₀, в которой мы абстрагируем Int в любой тип:

value g = all[b] all[a £ {one: b}] fun(x: a) x.one

g[Int][{one: Int, two: Bool}]({one=3, two=true})

где all[b]e – сокращение для all[b £ Top] e. Новая функция g не может быть выражена при помощи одного параметрического полиморфизма или одного наследования. Написать такую функцию позволит только их комбинация, реализуемая при помощи ограниченных кванторов.

Пока что ограниченные кванторы не дали нам ничего особенного, так как g₀ можно перефразировать как f_n, а g – как f, притом, что мы разрешаем включение типов при передаче параметров. Но ограниченные кванторы действительно более выразительны, как показано в следующем примере.

Необходимость в ограниченных кванторах очень часто возникает в объектно–ориентированном программировании. Предположим, что у нас есть следующие функции и типы:

type Point = { x : Int, y : Int }

value moveX₀ = fun(p : Point, dx : Int) p.x := p.x + dx; p

value moveX = all[P £  Point] fun(p : P, dx : Int) p.x := p.x + dx; p

Повторное использование таких функций, как moveX, для объектов, чей тип был неизвестен на момент определения функции moveX, типично для объектно-ориентированных языков. Если определить:

type Tile = { x : Int, y : Int, hor : Int, ver : Int }

мы можем захотеть использовать функцию moveX, чтобы двигать не точки, а элементы изображения. Однако если использовать более простую функцию moveX₀, можно предположить, что результат будет точкой, даже если параметр был элементом изображения, и мы разрешаем включение для аргументов функций. Следовательно, передавая элемент изображения через функцию moveX₀, мы потеряем информацию о типе, и например, мы не можем в дальнейшем возвращать в качестве результата функции значение поля hor.

Ограниченная квантификация позволяет лучше выражать зависимости ввода/вывода: тип результата функции moveX будет таким же, как и у ее аргумента, к какому подтипу Point он не принадлежал бы. Следовательно, мы можем применить moveX к элементу изображения и получить элемент изображения обратно без потери информации о типе.

moveX[Tile]({x=0,y=0,hor=1,ver=1},1).hor

Это показывает, что ограниченная квантификация полезна даже в отсутствие подходящего параметрического полиморфизма для адекватного выражения отношений подтипов.

Ранее мы видели, что параметрический полиморфизм может быть либо явным (с использованием кванторов всеобщности) или неявным (с помощью свободно типизированных переменных, неявно квантифицированных). Здесь мы имеем похожую ситуацию, где наследование может также быть явным, с использованием ограниченной квантификации, или оставаться неявным в правилах включения для передачи параметров. В объектно-ориентированных языках параметры подтипов, как правило, неявные. Мы можем рассмотреть такие языки как сокрщенные версии языков использующих ограниченную квантификацию. Таким образом, ограниченная квантификация полезна не только для увеличения выразительной силы, но и для того, чтобы сделать явным механизмы параметров, через которые осуществляется наследование.

6.3. Сравнение с другими механизмами выделения подтипов

Как приведенные выше механизмы наследования соотносятся с имеющимися в Simula, Smalltalk и Lisp Flavors? Для многих случаев применения наследования соответствие не будет точным, хотя его и можно добиться, переформулировав изложенное. Другие случаи применения наследования симулировать не выйдет, особенно те, в которых упор делается на динамическую типизацию. С другой стороны, есть некоторые вещи, осуществимые при помощи ограниченной квантификации, но невыполнимые в некоторых объектно-ориентированных языках.

Для моделирования классов и подклассов используются записи. Записи сравниваются по структуре, и отношения (множественного) наследования имен и типов членов записи неявны. В Simula и Smalltalk классы сравниваются по именам, и отношения наследования явны; допустимо только единичное наследование. В Lisp Flavors доступно множественное наследование. Метаклассы Smalltalk в имеющейся среде эмулировать нельзя.

Записи используются для моделирования экземпляров классов. Записи нужно конструировать явно (нет примитива создания нового экземпляра класса Х), инициализируя их поля. Из этого вытекает, что разные записи одного типа могут иметь разные значения полей; это дает уровень гибкости, которого нет в Simula и Smalltalk. Simula проводит различие между членами классами, разделяя их на методы и поля. Методы должны разделяться всеми экземплярами класса, а значения полей уникальны для каждого экземпляра. Виртуальные методы Simula – это способ введения функциональных членов, которые могут иметь разное поведение, но должны все же выглядеть одинаково во всех подклассах этого класса. Smalltalk также проводит различие между методами, разделяемыми всеми экземплярами класса, и переменными экземпляров, локальными для этих экземпляров. В отличие от переменных Simula, объявляемых в классах, переменные экземпляров в Smalltalk – закрытые (private) и недоступны напрямую. Этого поведения можно легко добиться в нашей среде, ограничивая видимость локальных переменных с помошью методики статических областей видимости.

Для моделирования методов используются функциональные члены записей. Как уже отмечалось выше, члены записей концептуально привязаны к индивидуальным записям, а не к типам записей (хотя это можно оптимизировать в реализациях). В Simula и Smalltalk подкласс может автоматически наследовать методы своего суперкласса или переопределять их. В случае множественного наследования такой автоматический способ наследования методов создает проблемы, если одинаковые методы определены в нескольких суперклассах: какой именно следует наследовать? Мы решаем эту проблему, заставляя создавать записи явно. Во время создания записи нужно явно выбрать, какие значения полей должна содержать конкретная запись; нужно ли наследовать их, используя некие предопределенные функции (или значения), используемые при размещении других записей, или переопределить их, используя новую функцию (или значение). Все можно, пока соблюдаются ограничения типа.

Сообщение, отправленное объекту с некоторыми параметрами, транслируется в выбор функционального члена записи и его применение к параметрам. Это очень похоже на то, что делается в Simula, а в Smalltalk, чтобы ассоциировать имена сообщений с реальными методами, применяется сложная процедура связывания имен. Simula может статически вычислить точное местоположение переменной или операции в экземпляре. Smalltalk вынужден выполнять динамический поиск, который можно оптимизировать, кешируя недавно использованные методы. Наш вариант имеет промежуточную сложность: из-за множественного наследования нельзя статически определить точное местоположение поля в записи, но кеширование может в среднем обеспечить почти константное вряемя доступа к полю, и обеспечивает константное время в программах, использующих только единичное наследование.

Концепция self в Smalltalk, соответствующая this в Simula (экземпляр класса, ссылающийся на собственные методы и переменные), может быть симулирована без введения каких-либо специальных конструкций. Это можно сделать с помощью рекурсивного определения записей, так, чтобы обычная переменная self (хотя можно использовать и другое имя) рекурсивно ссылалась на саму запись. Концепцию super из Smalltalk (экземпляр класса, ссылающийся на методы непосредственного суперкласса), а также сходные конструкции Simula (qua) и Flavors нельзя симулировать, так как они предполагают явную иерархию классов.

В Simula есть особая конструкция inspect, в сущности являющаяся оператором выбора класса объекта. У нас нет способа эмулировать это напрямую; однако выясняется, что inspect часто используется потому, что в Simula нет типов variant. Variant-типы в Simula получаются за счет объявления всех вариаций как подклассов (зачастую) фиктивного класса и последующего использования inspect с объектами этого класса. Поскольку у нас variant-ы есть, нам нужно только перефразировать соответствующие классы и подклассы Simula как variant-ы, а затем использовать для выбора обычный case.

В Smalltalk и Lisp Flavors есть некоторые идиомы, которые нельзя воспроизвести, поскольку для них практически невозможна статическая проверка типов. Например, во Flavors можно спросить, поддерживает ли объект сообщение (хотя можно переписать некоторые из таких ситуаций с использованием variant-типов). В общем, трудно тягаться с вольностями свободно типизированных языков, но в предыдущих разделах мы показали, что полиморфизм может далеко зайти в обеспечении гибкости, а ограниченная квантификация может распространить эту гибкость на случаи наследования.

6.4. Связанная экзистенциальная квантификация и частичная абстракция

Покончив с кванторами всеобщности, мы можем изменить кванторы существования типов, ограничив экзистенциальные переменные подтипами некоторого типа:

$a £  t. t'

Мы получим нотацию $a. t как сокращение для $a ≤ Top. t.

Ограниченные экзистенциально квантифицированные типы позволяют выражать частично абстрактные типы: хотя а абстрактно, мы знаем, что это – подтип t, таким образом, оно не более абстрактно, чем t. Если само t – это абстрактный тип, мы знаем, что эти два типа находятся в отношениях подтипов.

Это можно увидеть в следующем примере, где мы используем версию конструкции pack, измененную для использования ограниченных экзистенциально квантифицированных типов:

pack [a ≤ t = t' in t''] e

Предположим, что у нас есть два абстрактных типа, Point и Tile, и мы хотим их использовать и заставить взаимодействовать между собой. Предположим также, что мы хотим, чтобы Tile был подтипом Point, но мы не хотим знать, почему включение выполняется, поскольку хотим использовать их абстрактно. Такие требования мы можем выполнить с помощью следующего определения:

type Tile = $P. $T £ P. TileWRT2[P,T]

Следовательно, есть такой тип P (point), что существует тип T (tile), подтип P, поддерживающий операцию tile. Точнее:

type TileWRT2[P,T] =

{

  mktile: (Int * Int * Int * Int) → T,

  origin: T → P,

  hor: T → Int,

  ver: T → Int

}

type TileWRT[P] = $T ≤ P. TileWRT2[P,T]

type Tile = $P. TileWRT[P]

Следующим образом можно создать пакет tile, где конкретное представление точек и элементов изображения соответствует приведенным в предыдущих разделах:

type PointRep = {x:Int,y:Int}

type TileRep = {x:Int,y:Int,hor:Int,ver:Int}

pack [P = PointRep in TileWRT[P]]

pack [T ≤ PointRep = TileRep in TileWRT2[P,T]]

{

  mktile = fun(x:Int,y:Int,hor:Int,ver:Int) <x=x,y=y,hor=hor,ver=ver>,

  origin = fun(t:TileRep) t,

  hor = fun(t:TileRep) t.hor,

  ver = fun(t:TileRep) t.ver

}

Заметьте, что origin возвращает TileRep (ожидалось PointRep), но элементы изображения можно рассматривать как точки.

Функция, использующая абстрактные элемениты изображения, может рассматривать их как точки, хотя как представлены элементы изображения и точки, и почему элементы изображения – это подтипы точек, неизвестно:

fun(tilePack:Tile)

  open tilePack as t [pointRep] [tileRep]

    let f = fun(p:pointRep) ...

    in f(t.tile(0,0,1,1))

В языках с наследованием типов и абстрактными типами естественна возможность распространения наследования на абстрактные типы без необходимости раскрытия представлений типов. Как мы уже видели, ограниченные кванторы существования могут разъяснить эти ситуации и достичь полной интеграции наследования и абстракции.

7. Проверки типов и
выведение типов

В традиционных языках программирования компилятор присваивает тип любому выражению и подвыражению. Однако программист не должен указывать тип каждого подвыражения каждого выражения: информацию о типах нужно указывать только в критических точках программы, а остальное выводится по контексту. Этот процесс вывода называется выведением типов. Обычно информация о типах приводится для локальных переменных, а также для аргументов и результатов функций. Если типы переменных и основных констант известны, типы выражений (expressions) и утверждений (statements) могут быть выведены.

Выведение типов в деревьях выражений обычно выполняется снизу вверх. Зная тип листьев (переменных и констант) и правила типов для способов комбинирования выражений в большие выражения можно вывести тип всего выражения. Чтобы это работало, достаточно объявлять тип заново вводимых переменных. Заметьте, что необязательно объявлять возвращаемый тип функции или тип инициализированной переменной:

fun (x:Int) x + 1

let x = 0 in x + 1

Язык ML ввел более совершенный способ выведения типов. В ML необязательно даже указывать тип заново вводимых переменных, так что можно просто написать:

fun (x) x + 1

Алгоритм выведения типов по-прежнему работает снизу вверх. Тип переменной исходно считается неизвестным. Выше в «х + 1» х будет исходно иметь тип а, где а – это новая переменная типа (новая переменная типа вводится для каждой из переменных в программе). Затем целочисленный оператор сложения задним числом заставит а стать эквивалентным Int. Это воплощение переменных типов выполняется с помощью алгоритма унификации Робинсона [Robinson 65], который заботится также о распространении информации по всем экземплярам этой переменной для выявления случаев ее неверного использования. Вводный курс в выведение полиморфных типов можно найти в [Cardelli 84a].

Использование этого алгоритма выведения не ограничено полиморфными языками. Его можно ввести в любой мономорфный типизированный язык, с тем ограничением, что в конце проверки типов все переменные типов должны исчезнуть. Выражения наподобие fun (x) x будут неоднозначны, и чтобы эту неоднозначность устранить, придется писать что-то вроде fun (x:Int) x.

Лучший из известных алгоритмов выведения типов используется в ML и аналогичных языках. Это равнозначно заявлению, что лучшее из того, что мы умеем – это выведение типов для систем типов с небольшой экзистенциальной квантификацией, без выделения подтипов, и с ограниченной (но весьма мощной) формой универсальной квантификации. Более того, во многих расширениях системы типов ML было показано, что проблема проверки типов неразрешима.

Выведение типов сводится к проверке типов, если в программе так много информации о типах, что задача выведения типов становится тривиальной. Точнее, о проверке типов можно говорить, если все выражения типов, задействованные при проверке, уже явно содержатся в тексте программы, т.е., когда нет необходимости генерировать новые выражения типов при компиляции, и все что нужно – обеспечить соответствие существующим выражениям типов.

Мы, скорее всего, не можем надеяться отыскать полностью автоматический алгоритм выведения типов для системы типов, представленной в этой статье. Однако проблема проверки типов для этой системы оказывается очень простой, учитывая объем информации о типах, которая должна содержаться в каждой программе. Это, возможно, самое важное свойство этой системы типов: она очень выразительна при отсутствии каких-либо серьезных проблем проверки типов.

На самом деле есть одна проблема, общая для всех полиморфных языков, и касающаяся сторонних эффектов проверок типов. Придется наложить некоторые ограничения, чтобы предотвратить нарушение системы типов при сохранении и выборке полиморфных объектов из памяти. Примеры можно найти в [Gordon 79] и [Albano 83]. Есть несколько практических решений этой проблемы [Damas 84] [Milner 84], расплачивающихся гибкостью за сложность проверки типов.

Рисунок 2. Классификация систем типов.

8. Иерархическая классификация системы типов

Системы типов можно классифицировать по операторам типов, допускаемых ими. На рисунке 2 приведена (частично) диаграмма систем типов, упорядоченная по обобщенности. Каждый прямоугольник на диаграмме означает конкретно определенную систему типов; другие системы типов могут угодить в прмежутки между ними. Внизу каждого прямоугольника перечислены операторы типов, имеющиеся в системе типов (двигаясь снизу вверх, мы показываем только новые операторы). В верхней части каждого прямоугольника находится название системы типов, а в середине набор возможностей, которые она может моделировать (опять же, двигаясь снизу вверх, мы показываем только новые возможности). Диаграмму можно сделать более симметричной, но тогда она менее точно будет отражать структуру существующих классов языков.

Это классификация систем типов, а не языков. Конкретный язык может и не попасть в какую-то конкретную точку этой диаграммы, поскольку может иметь возможности, помещающие его на разные уровни и в разные точки диаграммы. Кроме того, системы типов существующих языков редко попадают в одну из отмеченных нами точек; чаще они обладают комбинацией возможностей, помещающий их где-то между точками.

Внизу находятся простые системы типов первого порядка, с декартовыми произведениями, несвязными суммами и функциональными пространствами первого порядка, variant-ами и процедурами первого порядка, соответственно. Знак ° означает неполное использование более общего оператора типа.

Системы типов первого порядка эволюционировали в системы типов высшего порядка (слева) и системы типов, основанные на наследовании (справа). Слева можно найти Algol 68, мономорфный язык высшего порядка. Справа находится Simula 67, язык с единичным наследованием, а выше – языки с множественным наследованием (опять же, размещающиеся не совсем точно). Над этими двумя классами систем типов находятся системы наследования высшего порядка, как в Amber [Cardelli 85].

Языки высшего уровня развились в параметрические полиморфные языки. В них может использоваться ограниченная универсальная квантификация высшего уровня (система типов Милнера [Milner 78], с корнями в Curry [Curry 58] и Hindley [Hindley 69]) или общая универсальная квантификация (система типов Girard-Reynolds [Girard 71] [Reynolds 74]).

Выше справа находятся системы типов с абстракцией типов, характеризуемая экзистенциальной квантификацией. Объединение кванторов всеобщности и существования дает систему типов SOL [Mitchell 85], которую можно использовать для объяснения основных возможностей модулей.

Остающиеся наверху пункты имеют отношение к включению. Мы показали, что ограниченные кванторы всеобщности нужны для моделирования объектно-ориентированного программирования, а ограниченные кванторы существования нужны для смешивания наследования с абстракцией данных.

Трех мощных концепций (включения, универсальной и экзистенциальной квантификации) достаточно для объяснения большинства возможностей программирования. При совместном использовании они позволяют гораздо больше, чем большинство существующих языков. Мы делали все возможное, чтобы обеспечить простоту проверки типов. Но это не полная картина. Многие интересные системы типов лежат значительно выше нашей диаграммы [Reynolds 85]. Они включают теорию конструкций [Coquand 85], зависимые типы [Martin-Löf 80], языки Pebble [Burstall 84] и DL [MacQueen 84b].

Есть выгоды в продвижении еще выше: Pebble и DL имеют более общий подход к параметрическим модулям; зависимые типы обладают практически неограниченной выразительной мощью. Но имеются и дополнительные трудности, которые, увы, отражаются на сложности проверок типов. Самая высшая точка нашей диаграммы, таким образом, – это подходящее место, чтобы остановиться, получить некоторый опыт, и решить, стоят ли дополнительные трудности дополнительной мощи.

9. Выводы

Расширенное λ-исчисление поддерживает системы типов с очень богатой структурой типов в функциональной среде. Оно позволяет моделировать такие же, и даже более богатые системы типов, чем имеющиеся в реальных языках программирования. Оно достаточно выразительно для моделирования абстракций данных Ада и классов объектно-ориентированных языков. Его возможность вычислений над типами лишь немногим слабее возможности вычислений над значениями.

Моделируя структуры типов и модулей реальных языков программирования в расширенном λ-исчислении, мы получаем понимание их абстрактных свойств независимо от индивидуальных свойств языков программирования, в которых они могут быть использованы. И наоборот, мы можем рассматривать структуры типов и модулей реальных языков программирования как «синтаксический сахар» для расширенного λ-исчисления.

Мы начали с типизированного λ-исчисления и расширили его такими примитивными типами, как Int, Bool, String, и конструкторами типов для пар, записей и variant-ов.

Универсальная квантификация использовалась для моделирования параметрического полиморфизма, а экзистенциальная квантификация – для моделирования абстракций данных. Практическое применение экзистенциальной квантификации показано на примере моделирования пакетов Ада с закрытыми типами данных. Польза комбинации универсальной и экзистенциальной абстракции показана на примере обобщенного стека, использующего универсальную квантификацию для моделирования обобщенных параметров типов и экзистенциальную квантификацию для моделирования скрытых структур данных.

И универсальная и экзистенциальная квантификация становятся более интересными, если мы можем ограничить область изменчивости стоящей под квантором переменной. Ограниченная универсальная квантификация улучшает абстракцию данных, позволяя определять отношения подтипов между абстрактными типами.

Понимание, что и поддиапазоны целых чисел, и подтипы, определяемые наследованием, – это случаи полиморфизма включения, расширяет применимость ограниченной квантификации к обоим этим случаям. Такие случаи подтипов записей, как {a:T1} ≤ {a:T1, b:T2}, в этом отношении особенно интересны. Это позволяет считать, что тип записи, полученный добавлением полей к существующему типу записи – это подтип данного типа.

Такие типы, как Cars, можно смоделировать с помощью типов-записей, чьи поля – это набор атрибутов, применимых к автомобилям. Такие подтипы, как Toyotas, можно смоделировать с помощью типов записей, включающих все поля записей Car и дополнительные поля для операций, применимых только к Toyotas. Множественное наследование можно в общем смоделировать с помощью подтипов записей.

Записи с функциональными членами – это очень мощный механизм для определения модулей, особенно в комбинации с механизмами сокрытия информации, реализуемыми через функциональные типы. Включение типов записей дает парадигму наследования типов и может использоваться как основа для дизайна строго типизированных объектно-ориентированных языков с множественным наследованием. Несмотря на то, что в статье мы использовали унифицированный язык (Fun), мы не предоставляем дизайн практического языка программирования. В дизайне языка есть много вопросов, касающихся читаемости, простоты использования и прочего, чего мы не касались.

Fun предоставляет среду для классификации и сравнения существующих языков, а также дизайна новых. Из-за неуклюжести мы не предлагаем его в качестве языка программирования, но как основа для такового он может сгодиться.

Ссылки

§         [Aho 85] A.V.Aho, R.Sethi, J.D.Ullman: Compilers. Principles, techniques and tools, Addison-Wesley 1985.

§         [Albano 85] A.Albano, L.Cardelli, R.Orsini: Galileo: a strongly typed, interactive conceptual language, Transactions on Database Systems, June 1985, 10(2), pp. 230-260.

§         [Booch 83] G. Booch, Software Engineering with Ada, Benjamin Cummings 1983.

§         [Bruce 84] K.B.Bruce, R.Meyer: The semantics of second order polymorphic lambda calculus, in Sematics of Data Types, G.Kahn, D.B.MacQueen and G.Plotkin Ed. Lecture Notes in Computer Science 173, Springer-Verlag, 1984.

§         [Burstall 80] R.Burstall, D.MacQueen, D.Sannella: Hope: an experimental applicative language, Conference Record of the 1980 LISP Conference, Stanford, August 1980, pp. 136-143.

§         [Burstall 84] R.Burstall, B.Lampson, A kernel language for abstract data types and modules, in Sematics of Data Types, G.Kahn, D.B.MacQueen and G.Plotkin Ed. Lecture Notes in Computer Science 173, Springer-Verlag, 1984.

§         [Cardelli 84a] L.Cardelli: Basic polymorphic typechecking, AT&T Bell Laboratories Computing Science Technical Report 119, 1984. Also in "Polymorphism newsletters", II.1, Jan 1984.

§         [Cardelli 84] L.Cardelli: A semantics of multiple inheritance, in Sematics of Data Types, G.Kahn, D.B.MacQueen and G.Plotkin Ed. Lecture Notes in Computer Science n.173, Springer-Verlag 1984.

§         [Cardelli 85] L.Cardelli: Amber, Combinators and Functional Programming Languages, Proc. of the 13th Summer School of the LITP, Le Val D'Ajol, Vosges (France), May 1985.

§         [Coquand 85] T.Coquand, G.Huet: Constructions: a higher order proof system for mechanizing mathematics, Technical report 401, INRIA, May 1985.

§         [Curry 58] H.B.Curry, R.Feys: Combinatory logic, North-Holland, Amsterdam, 1958.

§         [Damas 82] L.Damas, R.Milner: Principal type-schemes for functional programs, Proc. POPL 1982, pp.207-212.

§         [Damas 84] PhD Thesis, Dept of Computer Science, University of Edinburgh, Scotland.

§         [Demers 79] A.Demers, J.Donahue: Revised Report on Russell, TR79-389, Computer Science Department, Cornell University, 1979.

§         [D.O.D. 83] US Department of Defense: Ada reference manual, ANSI/MIS-STD 1815, Jan 1983.

§         [Fairbairn 82] J.Fairbairn: Ponder and its type system, Technical report No 31, Nov 82, University of Cambridge, Computer Laboratory.

§         [Girard 71] J-Y.Girard: Une extension de l'interprétation de Gödel a l'analyse, et son application à l'élimination des coupures dans l'analyse et la théorie des types, Proceedings of the second Scandinavian logic symposium, J.E.Fenstad Ed. pp. 63-92, North-Holland, 1971.

§         [Goldberg 83] A.Goldberg, D.Robson: Smalltalk-80. The language and its implementation, Addison-Wesley, 1983.

§         [Gordon 79] M.Gordon, R.Milner, C.Wadsworth. Edinburgh LCF, Lecture Notes in Computer Science, n.78, Springer-Verlag, 1979.

§         [Hendler 86] J.Hendler, P.Wegner: Viewing object-oriented programming as an enhancement of data abstraction methodology, Hawaii Conference on System Sciences, January 1986.

§         [Hook 84] J.G.Hook: Understanding Russell, a first attempt, in Sematics of Data Types, G.Kahn,

§         D.B.MacQueen and G.Plotkin Ed. Lecture Notes in Computer Science 173, pp. 51-67, Springer-Verlag, 1984.

§         [Hindley 69] R.Hindley: The principal type scheme of an object in combinatory logic, Transactions of the American Mathematical Society, Vol. 146, Dec 1969, pp. 29-60.

§         [Liskov 81] B.H.Liskov: CLU Reference Manual, Lecture Notes in Computer Science, 114, Springer-Verlag, 1981.

§         [McCracken 84] N.McCracken: The typechecking of programs with implicit type structure, in

§         Semantics of Data Types, Lecture Notes in Computer Science n.173, pp. 301-316, Springer-Verlag, 1984.

§         [MacQueen 84a] D.B.MacQueen, G.D.Plotkin, R.Sethi: An ideal model for recursive polymorphic types, Proc. Popl 1984. Also to appear in Information and Control.

§         [MacQueen 84b] D.B.MacQueen: Modules for Standard ML, Proc. Symposium on Lisp and Functional Programming, Austin, Texas, August 6-8 1984, pp 198-207. ACM, New York.

§         [MacQueen 86] D.B.MacQueen: Using dependent types to express modular structure, Proc. POPL 1986.

§         [Martin-Löf 80] P.Martin-Löf, Intuitionistic type theory, Notes by Giovanni Sambin of a series of lectures given at the University of Padova, Italy, June 1980.

§         [Matthews 85] D.C.J.Matthews, Poly manual, Technical Report No. 63, University of Cambridge, Computer Laboratory, 1985.

§         [Milner 78] R.Milner: A theory of type polymorphism in programming, Journal of Computer and System Science 17, pp. 348-375, 1978.

§         [Milner 84] R.Milner: A proposal for Standard ML, Proc. Symposium on Lisp and Functional Programming, Austin, Texas, August 6-8 1984, pp. 184-197. ACM, New York.

§         [Mitchell 79] J.G.Mitchell, W.Maybury, R.Sweet: Mesa language manual, Xerox PARC CSL-79-3, April 1979.

§         [Mitchell 84] J.C.Mitchell: Type Inference and Type Containment, in Semantics of Data Types, Lecture Notes in Computer Science 173, 51-67, Springer-Verlag, 1984.

§         [Mitchell 85] J.C.Mitchell, G.D.Plotkin: Abstract types have existential type, Proc. Popl 1985.

§         [Reynolds 74] J.C.Reynolds: Towards a theory of type structure, in Colloquium sur la programmation, pp. 408-423, Springer-Verlag Lecture Notes in Computer Science, n.19, 1974.

§         [Reynolds 85] J.C.Reynolds: Three approaches to type structure, Mathematical Foundations of Software Development, Lecture Notes in Computer Science 185, Springer-Verlag, Berlin 1985, pp. 97-138.

§         [Robinson 65] J.A.Robinson: A machine-oriented logic based on the resolution principle, Journal of the ACM, vol. 12, no. 1, Jan. 1956, pp. 23-49.

§         [Schmidt 82] E.E.Schmidt: Controlling large software development in a distributed environment, Xerox PARC, CSL-82-7, Dec. 1982.

§         [Scott 76] D.Scott: Data types as lattices, SIAM Journal of Computing, Vol 5, No 3, September 1976, pp. 523-587.

§         [Solomon 78] M.Solomon: Type Definitions with Parameters, Proc. POPL 1978, Tucson, Arizona.

§         [Strachey 67] C.Strachey: Fundamental concepts in programming languages, lecture notes for the International Summer School in Computer Programming, Copenhagen, August 1967.

§         [Welsh 77] J.Welsh, W.J.Sneeringer, C.A.R.Hoare: Ambiguities and insecurities in Pascal, Software Practice and Experience, November 1977.

§         [Wegner 83] P.Wegner: On the unification of data and program abstraction in Ada, Proc POPL 1983.

§         [Weinreb 81] D.Weinreb, D.Moon: Lisp machine manual, Fourth Edition, Chapter 20: Objects, message passing, and flavors, Symbolics Inc., 1981.

§         [Wirth 83] N.Wirth: Programming in Modula-2, Springer-Verlag 1983.

Copyright © 1994-2016 ООО "К-Пресс"

Copyright © 1994-2016 ООО "К-Пресс"